Elastic materials having the capacity to dissipate the mechanical energy due to viscous effects are characterized as viscoelastic materials.
For multi-axial stress state, the constitutive relation can be written as:

where: e(bar) and φ are the deviatoric and volumetric strain, G(t - τ) and K(t - τ) are shear and bulk relaxation functions.
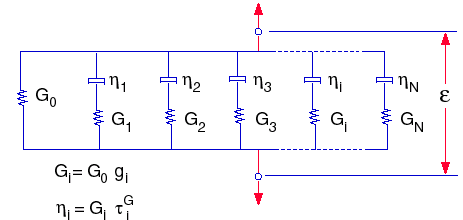
The relaxation functions can then be represented by the mechanical model which is usually referred to as a Generalized Maxwell Model having the expressions:

where: G0 = E / 2(1+ ν), initial shear modulus (t=0)
and K0= E / 3(1 -2ν), initial bulk modulus (t=0)
gi, ki, τiG, and τiK are the i-th shear and bulk moduli and corresponding times.
The effect of temperature on the material behavior is introduced through the time-temperature correspondence principle. The mathematical form of the principle is:

where γt is the reduced time and γ is the shift function. The WLF (Williams-Landel-Ferry) equation is used to approximate the function:
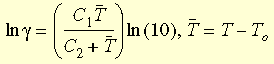
where T0 is the reference temperature which is usually picked as the Glass transition temperature; C1 and C2 are material dependent constants.
| Parameter |
Material Property |
|---|
| Linear Elastic Parameters |
Elastic modulus
in X |
| Poisson's ratio
in XY |
| Shear modulus
in XY |
| Relaxation Function Parameters |
Shear relaxation modulus (1 to 8) (represent g1, g2, ...,g8 in the Generalized Maxwell Model equations)
|
| Time values (Shear relaxation modulus 1 to 8) (represent τ1g, τ2g,..., τ8g in the Generalized Maxwell Model equations) |
| Bulk Relaxation Modulus (1 to 8) |
| Time values (Bulk relaxation modulus 1 to 8) (represent τ1k, τ2k,..., τ8k in the Generalized Maxwell Model equations) |
| WLF Equation Parameters
|
Glassy Transition Temperature (represents T0 in the WLF equation)
|
| First Constant for Williams-Landel-Ferry equation (represents C1 in the WLF equation)
|
| Second Constant for Williams-Landel-Ferry equation (represents C2 in the WLF equation)
|
When defining a shear or bulk relaxation curve under the Tables & Curves tab, the first point of the curve is the G1 or K1 moduli at time t1. At time t = 0, the program automatically computes G0 or K0 from the Elastic modulus and Poisson's ratio.
The viscoelastic material model can be used with the draft and high quality solid and thick shell elements.