应力周期的交替应力幅度计算为周期中应力范围的一半。由应力循环所导致的损坏量不但取决于交替应力,也取决于平均应力。例如,下面的两个循环具有相同的交替应力,但由于它们的平均应力不同,因此它们所导致的损坏量也不同。

对于导致失效的循环,平均应力的效果可通过下面称为 Haigh 图的图表加以说明。
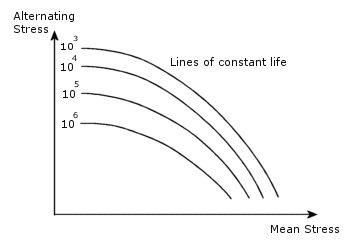
仅当载荷为完全可逆时平均应力才为零。最直观的示例是所提供的 S-N 曲线具有与负载相同的 R-比率的情况。在这种情况下,由于无需进行应力纠正,因此将会直接使用 S-N 曲线。如果定义的 S-N 曲线具有不同的 R 比率,则软件通过在曲线之间的线性插值来计算平均应力。如果只提供了一条 S-N 曲线,并且其 R-比率不同于负载的 R-比率,则此时需要进行纠正。
该程序始终使用 von Mises 应力来计算平均应力。由于 von Mises 是正数,因此程序会分配第一个主要平均应力给它,以计算关联的平均应力。
定义
要讨论纠正方法,我们可以定义应力循环的下列变量:
Smax = 最大应力
Smin = 最小应力
ΔS = 应力范围 = Smax - Smin
Sa = 交替应力 = (Smax - Smin)/2
Smean = 平均应力 = (Smax + Smin)/2
R = 应力比率 = Smin/Smean
A = 振幅比 = Sa/Smean
一些常见负载的应力和振幅比如下所示:
| 负载类型
|
应力和振幅比
|
|---|
| 完全反转
|
R = -1,A = 无穷大
|
| 零到最大值
|
R = 0,A = 1
|
| 零到最小值
|
R = 无穷大,A=-1
|
纠正方法
在下面:
Sca = 纠正的交替应力(基于零平均应力);
Sy = 屈服应力,以及
Su = 终极强度
该软件提供以下方法计算 S
ca:
| 方法
|
方程式
|
|---|
| 1. Goodman 方法 - 通常适合于脆性材料:
|
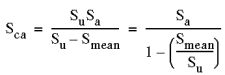 |
| 2. Gerber 方法 - 通常适合于延性材料
|
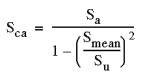 |
| 3. Soderberg 方法 - 通常最保守
|
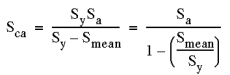 |
无论振幅可变还是恒定,该软件除了各周期的交替应力之外,还会计算其平均应力,然后使用指定准则评估纠正的应力。