Blatz-Ko 应变能密度函数对于建立可压缩聚氨酯泡沫类型橡胶的模型非常有用,可以表示为:
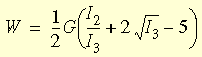
其中:
- G = E / 2(1+ν) 是无限小变形下的抗剪模量,E 是杨氏弹性模量,ν 是泊松比。
- Ik (k=1,..3) 是 Cauchy-Green 变形张量的不变量 C=Ik ©)
- C = 2ε +I,ε 是拉格朗日应变张量,I 是单位矩阵。
上述表达式只包含一个材料常量 G,由于 ν = 0.25 代表 Blatz-Ko 模型,唯一被看成杨氏模量的材料属性。
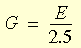
目前只有实体单元(草稿和高品质单元)支持 Blatz-Ko 模型。
所选 Blatz-Ko 模型是 Blatz 和 Ko (1962) 所得到的表达式的简化形式,表达式用于建立高度可压缩的聚氨酯泡沫橡胶的变形模型。应变能由下列表达式近似计算:
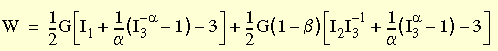
其中
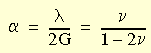
随后提出了弹性势的此三个参数系列的特定形式,其中假设了常量 α、β 和 ν 的下列数值:α = 0.5,β = 0 和 ν = 0.25。