La funzione della densità dell'energia di deformazione Blatz-Ko è solitamente utilizzata per la modellazione di gomme in poliuretano espanso e può essere espressa come:
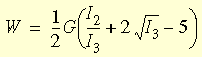
dove:
- G = E / 2(1+ν) è il modulo di taglio sotto deformazioni infinitesimali, E è il modulo elastico di Young, ν è il coefficiente di Poisson
- Ik (k=1,...3) sono le invarianti del tensore di deformazione di Cauchy-Green C=Ik ©)
- C = 2ε +I , ε è il tensore di deformazione di Lagrange e I è la matrice di identità.
L'espressione sopra riportata contiene solo una costante di materiale G. Poiché ν = 0,25 per il modello Blatz-Ko, la sola proprietà del materiale che viene considerata è il modulo di Young.
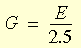
Il modello Blatz-Ko è attualmente supportato solo da elementi solidi (qualità bozza e alta).
Il modello Blatz-Ko selezionato è un modulo semplificato dell'espressione ottenuta da Blatz e Ko (1962) per la modellazione della deformazione di una gomma in poliuretano espanso altamente compresso. L'energia di deformazione è stata approssimata dalla seguente espressione:
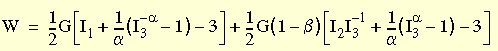
dove
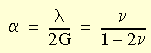
Successivamente, è stato proposto un modulo specifico di questa famiglia di tre parametri di potenziale elastico in cui sono presupposti i seguenti valori delle costanti α, β e ν: α = 0,5, β = 0 e ν = 0,25.