Expand IntroduzioneIntroduzione
Expand AmministrazioneAmministrazione
Expand Interfaccia utenteInterfaccia utente
Expand Nozioni fondamentali su SolidWorksNozioni fondamentali su SolidWorks
Expand Migrazione da 2D a 3DMigrazione da 2D a 3D
Expand AssiemiAssiemi
Expand CircuitWorksCircuitWorks
Expand ConfigurazioniConfigurazioni
Expand SolidWorks CostingSolidWorks Costing
Expand Design CheckerDesign Checker
Expand Studi progettuali in SolidWorksStudi progettuali in SolidWorks
Expand Disegni e dettagliDisegni e dettagli
Expand DFMXpressDFMXpress
Expand DriveWorksXpressDriveWorksXpress
Expand FloXpressFloXpress
Expand Importazione ed esportazioneImportazione ed esportazione
Expand Visualizzazione modelloVisualizzazione modello
Expand Progettazione di stampiProgettazione di stampi
Expand Studi del movimentoStudi del movimento
Expand Parti e funzioniParti e funzioni
Expand InstradamentoInstradamento
Expand LamieraLamiera
Collapse SimulationSimulation
Expand SimulationXpressSimulationXpress
Expand Tecniche di schizzoTecniche di schizzo
Expand Prodotti SustainabilityProdotti Sustainability
Expand SolidWorks UtilitiesSolidWorks Utilities
Expand TolerancingTolerancing
Expand TolAnalystTolAnalyst
Expand ToolboxToolbox
Expand SaldatureSaldature
Expand Workgroup PDMWorkgroup PDM
Expand DiagnosticaDiagnostica
Glossario
Nascondi Sommario

Formula del modello in nitinol

Poiché il nitinol viene utilizzato solitamente per la sua capacità di resistenza alle deformazioni finite, per questo modello è impiegata la teoria della forte deformazione che utilizza le deformazioni logaritmiche insieme alla formula di Lagrange.

Di conseguenza, il modello costitutivo è costruito in modo da correlare le deformazioni logaritmiche ed i componenti di sollecitazione di Kirchhoff. Tuttavia, in definitiva, la matrice costitutiva e il vettore della deformazione sono entrambi trasformati per presentare le sollecitazioni di Cauchy (reali).

Material_nitinol_loading_unloading.gif

σst1, σft1

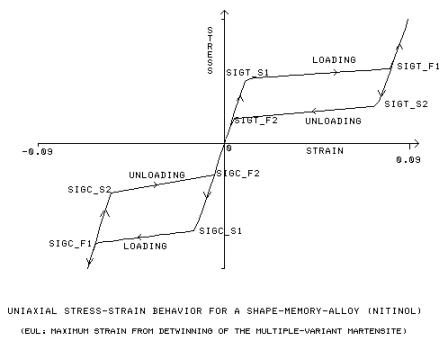
Sollecitazione di snervamento iniziale e finale per il carico di trazione [SIGT_S1, SIGT_F1]

σst2, σft2

Sollecitazione di snervamento iniziale e finale per lo scarico di trazione [SIGT_S2, SIGT_F2]

σsc1, σfc1

Sollecitazione di snervamento iniziale e finale per il carico di compressione [SIGC_S1, SIGC_F1]

σsc2, σfc2

Sollecitazione di snervamento iniziale e finale per lo scarico di compressione [SIGC_S2, SIGC_F2]

eul

(Deformazione plastica di tensione massima) *(3/2)0,5

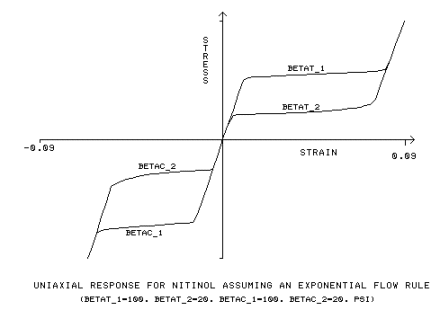
Material_nitinol_expon_law.gif
La regola di flusso esponenziale utilizza ulteriori valori costanti, βt1, βt2, βc1, βc2:

βt1

parametro del materiale, misurazione della velocità di trasformazione per il carico di trazione, [BETAT_1]

βt2

parametro del materiale, misurazione della velocità di trasformazione per lo scarico di trazione, [BETAT_2]

βc1

parametro del materiale, misurazione della velocità di trasformazione per il carico di compressione, [BETAC_1]

βc2

parametro del materiale, misurazione della velocità di trasformazione per lo scarico di compressione, [BETAC_2]

Il criterio di snervamento

Per la modellazione della possibilità della dipendenza dalla pressione di una trasformazione di fase, viene utilizzata una funzione di carico di tipo Drucker-Prager per il criterio di snervamento:

F(τ) = radq(2)*σ(bar) + 3*α*p
F - RIf = 0
dove
σ(bar) = sollecitazione effettiva
p = sollecitazione media (o pressione idrostatica)
α = radq(2/3) (σsc1 - σst1) / (σsc1 - σst1)
RfI = [ σfI(radq(2/3) + α)], I = 1 per il carico e 2 per lo scarico


Fornisci il feedback su questo argomento

SOLIDWORKS apprezza il feedback degli utenti relativamente alla presentazione, la precisione e l'esaustività della documentazione. Usare il modulo riportato di seguito per inviare i propri commenti e suggerimenti su questo argomento direttamente al nostro team della documentazione. Questo team non è in grado di rispondere a domande di natura tecnica. Fare clic qui per informazioni sul supporto tecnico.

* Obbligatoria

 
*Email:  
Oggetto:   Feedback sugli argomenti della guida
Pagina:   Formula del modello in nitinol
*Commento:  
*   Confermo di aver letto e accettato l'informativa sulla privacy che regola l'utilizzo dei miei dati personali da parte di Dassault Systèmes

Stampa argomento

Selezionare il contenuto da stampare:

x

L'utente utilizza una versione di Internet Explorer precedente alla versione 7. Per una visualizzazione ottimale, consigliamo di fare l'upgrade del proprio browser a Internet Explorer 7 o successiva.

 Non mostrare nuovamente questo messaggio
x

Versione contenuto guida Web: SOLIDWORKS 2014 SP05

Per disattivare la guida Web dall'interno di SOLIDWORKS e usare invece la guida locale, fare clic su ? > Usa la guida Web di SOLIDWORKS.

Per segnalare i problemi riscontrati con l'interfaccia e la funzionalità di ricerca della guida Web, contattare il rappresentante del supporto locale. Per fornire un feedback su singoli argomenti della guida, usare il link "Feedback su questo argomento" nella pagina del singolo argomento.

0.20.46