Pomocí harmonické analýzy lze počítat špičkovou odezvu systému v klidovém stavu v důsledku harmonických zatížení nebo základových buzení.
Harmonické zatížení P je vyjádřeno jako P = A sin (ωt + φ), kde: A je amplituda, ω je frekvence, t je čas a φ je fázový úhel. Vzorová harmonická zatížení o různých frekvencích w v závislosti na čase jsou zobrazena níže:
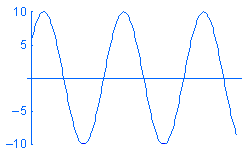
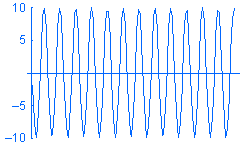
Ačkoli lze vytvořit studii modálního časového průběhu a určovat zatížení jako funkce času, přechodové změny v závislosti na čase nemusejí být vždy požadovány. V takových případech lze šetřit čas a zdroje vyřešením špičkové odezvy ustáleného stavu v požadovaném rozsahu provozních frekvencí pomocí harmonické analýzy.
Například motor upevněný na zkušební stolici přenáší harmonické zatížení na systém podpěr prostřednictvím šroubů. Podpůrný systém lze modelovat a určit harmonickou studii k vyhodnocení špičkových posunů, napětí atd. v ustáleném stavu pro rozsah provozních frekvencí daného motoru. Motor můžete přibližně zpracovat pomocí rozptýlené hmoty.

Po spuštění studie lze zobrazit špičková napětí, posuny, zrychlení, rychlosti a fázové úhly reakce v celém rozsahu provozních frekvencí.
Možnosti modálního, Rayleighova a složeného modálního tlumení jsou pro tento typ analýzy k dispozici.