Utilisez la relaxation inertielle pour calculer les contraintes et les déformations sur un corps libre qui accélère comme une fusée propulsée par son moteur, un avion en plein vol, ou une automobile en mouvement.
Si un modèle n'est pas soumis à des déplacements imposés appropriés, une petite force peut provoquer un mouvement de corps rigide. Même dans les cas où les forces appliquées sont théoriquement équilibrées, une petite force de déséquilibre peut résulter des approximations numériques faites lors de l'application des chargements au modèle.
Pour activer la relaxation inertielle, sélectionnez Utiliser la relaxation inertielle dans la boîte de dialogue Statique. Lorsque cette option est cochée, le programme applique automatiquement les forces d'inertie distribuées à tous les nœuds du modèle pour former un état équivalent d'équilibre statique.
Lorsque cette option est activée, vous pouvez résoudre les problèmes structurels sans appliquer de déplacements imposés ni activer l'option de raideur faible pour stabiliser le modèle et éviter les mouvements de corps rigide.

|
{F}t
|
Forces externes appliquées
|
|
{α}t
|
Accélération en translation due à l'inertie (à calculer)
|
|
ρ
|
Densité du matériau
|
|
v
|
Volume du matériau
|
L'équation ci-dessus mentionnée peut être représentée ainsi :
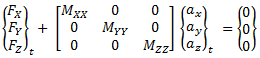
où Mxx, Myy et Mzz sont des masses totales dans les directions x, y et z et sont évaluées par une somme ligne-par ligne des matrices de masse élémentaires sur les degrés de liberté en translation. Une fois que Mxx, Myy, et Mzz sont évalués, l'équation produit les accélérations induites αx, αy, et αz qui sont appliquées comme un champ d'accélération à la solution.
La relaxation inertielle est également appliquée aux cas pour lesquels une force externe non équilibrée sur un corps élastique peut causer le mouvement du corps rigide. La force non équilibrée peut être équilibrée par les forces d'inertie distribuées induites par un champ d'accélération en translation.
L'option de relaxation inertielle est particulièrement pratique lorsque vous importez des chargements à partir de SolidWorks Motion. Dans ce cas, les chargements externes peuvent être légèrement déséquilibrés. La relaxation inertielle est basée sur le principe de D'Alembert, qui stipule que l'on peut transformer un corps rigide en accélération en un système statique équivalent par l'ajout de forces d'inertie et d'un moment d'inertie ou de couple.
Dans l'application Simulation, seul le champ en translation est pris en compte ; les rotations induites sont ignorées.