降伏基準は、次の形で記述できます: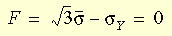
ここで
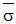
は有効応力、σ
Y は単軸試験の降伏応力です。 von Misesモデルは、金属の動作を記述するために使用できます。 この材料モデルを使用するにあたり、次の点に注意してください。
- 微小変位あるいは大変位が使用される場合、塑性ひずみは小さく仮定されます。
- 関連する流れ則が仮定されます。
- 等方性および運動学的硬化則のどちらも使用できます。等方性あるいは運動学硬化則の線形の組み合わせは、偏差空間の半径と降伏サーフェスの両方が、荷重の履歴に関して変化することができるとき、設定されます。
パラメータ RK は等方硬化性および運動学的硬化則の大きさを定義します。純等方硬化性では、パラメータ RK は値 0 を持ちます。 降伏サーフェスの半径は拡大されますが、その中心は偏差空間で固定されたままです。純移動硬化則では、パラメータ RK は値 1 を持ちます。降伏サーフェスの半径は、その中心は偏差空間で移動される間、一定に保たれます。
または可塑性のための多線形の一軸応力-ひずみ曲線を入力できます。 双線形応力-ひずみ曲線の定義では、降伏強さ、弾性係数、接線係数は、材料 ダイアログ ボックスを通して入力します。 多線形の応力-ひずみ曲線の定義では、応力-ひずみ曲線を定義する必要があります。

応力-ひずみ曲線を定義する場合、曲線の第 1 点は材料の降伏点とする必要があります。弾性係数、降伏強さなどの材料特性は、材料(Material)ダイアログ ボックスにある材料特性テーブルではなく、利用可能な応力-ひずみ曲線から取得されます。ただし、ポアソン比(NUXY)のみがテーブルから取得されます。
落下試験スタディは、可塑性のための双線形応力-ひずみ曲線のみ使用します。 多線形の応力-ひずみ曲線を定義し、落下試験スタディを実行した場合、ソルバで無視されます。
熱塑性解析を実行するために、双線形応力-ひずみ曲線を記述する降伏強さおよび弾性係数パラメータを温度曲線と関連付けることもできます。熱可塑性は、シェル要素では使用できません。
Huber-von Mises モデルは、固体(ドラフト精度、および高精度)および厚肉シェル(ドラフト精度、および高精度)を使用できます。
NR (ニュートン・ラプソン法) 反復法を使用することをお勧めします。
塑性材料の典型的な応力-ひずみ曲線:
