항복 기준은 다음과 같이 정의할 수 있습니다. 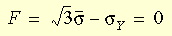
여기서,

은(는) 유효 응력이고 σ
Y은(는) 단축 테스트에서 얻은 항복 응력입니다. von Mises 모델을 사용하여 금속의 동작을 설명할 수 있습니다. 이런 재질 모델을 사용할 때 다음을 고려해야 합니다.
- 소변위 또는 대변위가 사용되는 경우 변형 가소성이 약간 있는 것으로 간주됩니다.
- 관련된 유동 규칙이 전제됩니다.
- 등방성 및 동역학 가공경화 규칙을 사용할 수 있습니다. 편차 공간 안의 반경과 항복 곡면 모두가 하중 기록과 관련하여 변할 수 있는 경우 등방성 및 동역학 가공경화의 선형 조합이 적용됩니다.
변수 RK가 동역학 및 등방성 가공경화의 균형을 정의합니다. 등방성 가공경화만일 경우, 변수 RK의 값은 0입니다. 항복 곡면의 반경이 확장되나 편차 공간에서 중심이 고정됩니다. 순수한 동역학적 경화일 경우, 파라미터 RK의 값은 1입니다. 편차 공간에서 중심이 이동할 수 있으나 항복 곡면의 반경은 일정하게 유지됩니다.
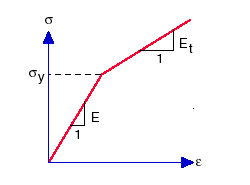
가소성을 나타내는 이중 또는 다중 선형 단축 응력-변형 곡선을 입력할 수 있습니다. 평형 응력-변형 곡선 정의의 경우, 항복 강도, 탄성 계수 및 탄젠트 계수는 재질 대화 상자에서 입력할 수 있습니다. 다중 선형 응력-변형 곡선 정의일 경우 응력-변형 곡선을 정의해야 합니다.
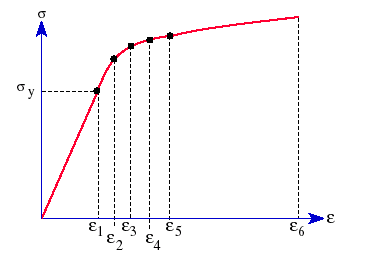
응력-변형 곡선을 정의할 때 곡선의 첫 번째 지점이 재질의 항복 지점이어야 합니다. 탄성 계수, 항복 응력 등과 같은 물성치는 응력-변형 곡선을 사용할 수 있는 경우 이 곡선에서 가져오며 재질 대화 상자의 물성치 테이블에서 가져오지 않습니다. 포아송비(NUXY)만 이 테이블에서 가져옵니다.
낙하/충격 해석 스터디에서는 가소성에 대한 평형 응력-변형 곡선만 사용할 수 있습니다. 다중 선형 응력 변형 곡선을 정의하고 낙하/충격 해석 스터디를 실행하는 경우, 솔버는 이를 무시합니다.
평행 응력-변형 곡선 설명에 대한 항복 응력 및 탄성 계수 파라미터를 온도 곡선과 결합하여 열가소성 해석을 수행할 수 있습니다. 열가소성은 쉘 요소에는 사용할 수 없습니다.
Huber-von Mises 모델을 솔리드(시험 품질 및 고품질)와 두꺼운 쉘 요소(시험 품질 및 고품질)와 함께 사용할 수 있습니다.
NR(Newton-Raphson) 반복 방법을 사용하는 것이 좋습니다.
플라스틱 재질의 일반적인 응력-변형 곡선: