Funkcja gęstości energii odkształcenia Ogdena jest zdefiniowana jako:
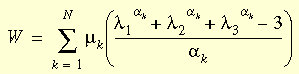
gdzie: λi są rozciągnięciami głównymi, αi i μi są stałymi materiałowymi, a N jest liczbą składników w funkcji. Jest ona uważana za jedną z najlepszych funkcji opisujących zakres dużych deformacji materiałów gumopodobnych.
Funkcja kary używana w wyrażeniu modelu Ogden przybiera formę funkcji używanej w modelu Mooney'a-Rivlina. Faktycznie użyta funkcja energii odkształcenia jest zmodyfikowaną funkcją Ogdena:
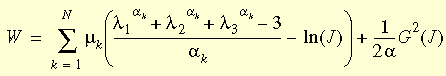
gdzie J jest stosunkiem zdeformowanej objętości do niezdeformowanej objętości, N jest liczbą składników w funkcji, G(J) = J2-1 oraz
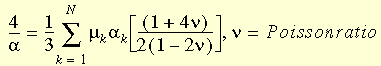
Modele trzyskładnikowe (zmodyfikowany model Ogden) są powszechnie stosowane. W programie dostępne są modele z maksymalnie 4 składnikami (N=4).
Oprócz wspomnianych wcześniej stałych materiałowych, wymagany jest również współczynnik Poissona. W większości przypadków zadowalające wyniki można uzyskać przypisując współczynnik Poissona z zakresu od 0.49 do 0.499. Dalsze zwiększanie współczynnika Poissona nie będzie miało istotnego wpływu na wyniki numeryczne, chyba że występuje znaczne odkształcenie wolumetryczne.
Gdy współczynnik Poissona jest bardzo bliski 0.5, może spowodować przerwanie rozwiązania z powodu ujemnych składników diagonalnych w macierzy sztywności lub braku konwergencji.
Właściwości materiałowe modelu Ogden określa się za pomocą okna dialogowego
Materiał. Wymagane wielkości:
- Współczynniki mocy materiału od pierwszego do czwartego (αi)
- Stałe materiałowe od pierwszej do czwartej (μi) (w zależności od liczby stałych).
- Współczynnik Poissona