Dependiendo de las configuraciones, el análisis no lineal puede requerir la entrada de curvas de tensión-deformación unitaria. Si se da el caso, la curva se debe introducir usando las definiciones correctas para tensión y deformación unitaria.
La siguiente tabla resume los tipos de tensión y deformación unitaria que se van a usar como entrada para la curva de tensión-deformación unitaria, según la opción de análisis y el tipo del modelo material utilizado.
| Opciones de análisis |
|---|
| Modelo de material |
Pequeñas deformaciones unitarias, Desplazamientos pequeños |
Pequeñas deformaciones unitarias, Grandes desplazamientos |
Grandes deformaciones unitarias, Grandes desplazamientos |
| Elástico no lineal |
Tensión verdadera, Deformación unitaria de ingeniería |
Tensión verdadera, Deformación unitaria de ingeniería |
No aplicable |
| Elastoplástico, Plasticidad de von Mises, Plasticidad de Tresca, Drucker Prager |
Tensión verdadera, Deformación unitaria de ingeniería |
Tensión verdadera, Deformación unitaria de ingeniería |
Tensión verdadera, Deformación unitaria logarítmica |
| Hiperelásticos: Mooney-Rivlin, Ogden, Blatz Ko |
Tensión de ingeniería, Cociente de estiramiento |
Tensión de ingeniería, Cociente de estiramiento |
Tensión de ingeniería, Cociente de estiramiento |
| Superelástico |
Tensión verdadera, Deformación unitaria logarítmica |
Tensión verdadera, Deformación unitaria logarítmica |
Tensión verdadera, Deformación unitaria logarítmica |
| Viscoelástico |
Tensión verdadera, Deformación unitaria de ingeniería |
Tensión verdadera, Deformación unitaria de ingeniería |
No aplicable |
Una vez finalizado el análisis, el resultado de la tensión es la tensión de Cauchy, que es la tensión verdadera en la geometría deformada.
El resultado de la deformación unitaria depende del modelo de material y la opción de la formulación de grandes o pequeñas deformaciones unitarias.
Para modelos elásticos no lineales: Plasticidad de von Mises, Plasticidad de Tresca, Drucker Prager, Superelástico y Viscoelástico, la opción de pequeñas deformaciones unitarias produce deformación unitaria de ingeniería; la opción de grandes deformaciones unitarias produce deformaciones unitarias logarítmicas.
|
Tensión y deformación unitaria verdadera
|
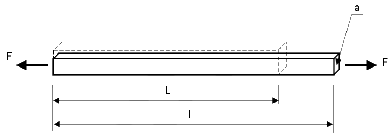
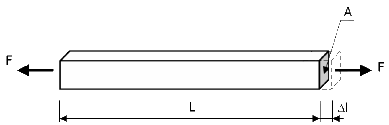
Si la deformación de una barra en tensión se vuelve importante, su área de sección transversal cambiará. Las definiciones de ingeniería tradicionales para tensión y deformación unitaria ya no son medidas precisas y nuevas, se introducen la tensión verdadera y la deformación unitaria verdadera. Los nombres alternativos para estas medidas son tensión de Cauchy, deformación unitaria logarítmica y deformación unitaria natural. La tensión verdadera es 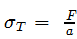 , donde a es el área de sección transversal deformada final.
La deformación unitaria verdadera es 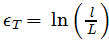 , donde l es la longitud final y L es la longitud inicial no deformada de la barra.
|
|
Tensión y deformación unitaria de ingeniería
|
La tensión de ingeniería (o tensión nominal)  , donde A es el área de sección transversal no deformada inicial.
La deformación unitaria de ingeniería (o deformación unitaria nominal) es 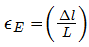 dónde Δl es la deformación de barra final.
|
- La deformación unitaria de ingeniería es una medida de deformación unitaria pequeña que no es válida una vez que la deformación unitaria del modelo ya no es "pequeña" (aproximadamente mayor del 5%). Deformación unitaria logarítmica, que es una medida de deformación unitaria no lineal que depende de la longitud final del modelo, se usa para simulaciones de deformaciones unitarias grandes.
- Para el modelo de material viscoelástico, la definición tensión frente a deformación unitaria se reemplaza por la función de relajación frente a tiempo.
- La extrapolación de la curva de tensión-deformación unitaria después de los últimos puntos de datos de la curva: para la definición de material elástico no lineal o plasticidad, los últimos puntos de datos se extrapolan linealmente para calcular pares de puntos de datos fuera de la curva de tensión-deformación unitaria definida.
-
Al definirse una curva de tensión-deformación unitaria, el primer punto de la curva debe ser el punto de flexibilidad del material. Las propiedades de material, como el módulo elástico, límite elástico, etc. se obtendrán de la curva de tensión-deformación unitaria cuando la misma se encuentre disponible y no de la tabla de propiedades de material, en el cuadro de diálogo Material. Sólo se tomará de la tabla el coeficiente de Poisson (NUXY).