彈性模型基於其黏彈性材料所特有的黏性效應,而能夠耗散力學能。
在多軸向應力狀態中,其本構關係式可如下表示:

其中︰ e(bar) 及 φ 是軸差及體積應變,G(t - τ) 和 K(t - τ) 是剪力及容積鬆弛函數。
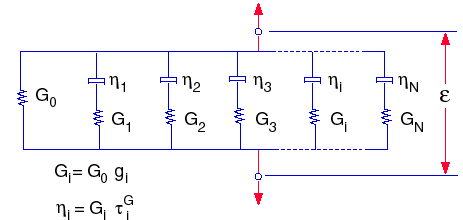
鬆弛函數又可由力學模型表示,該模型通常是指具有以下表達式的廣義麥斯威爾模型:

其中︰ G0 = E / 2(1+ ν),初始剪力模數 (t=0)
和 K0= E / 3(1 -2ν),初始容積模數 (t=0)
gi、ki、τiG 和 τiK 是 i-th 剪力與容積模數以及對應時間。
材料行為上的溫度效應係透過時間-溫度相依性原則代入。該原則的數學式為:

其中 γt 是減少的時間,而 γ 是轉換函數。 使用 WLF (Williams-Landel-Ferry) 方程式概算出下列函數:
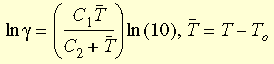
其中 T0 是參考溫度,通常是採用玻璃轉折溫度;C1 和 C2 是材料相依常數。
| 參數 |
材料屬性 |
|---|
| 線性彈性參數 |
X 方向彈性模數 |
| 在 XY 上的 Poisson 比 |
| XY 上的剪力模數 |
| 鬆弛函數參數 |
剪力鬆弛模數 (1 到 8) (表示廣義麥斯威爾模型方程式中的 g1、g2、…、g8)
|
| 時間值 (剪力鬆弛模數 1 到 8) (表示廣義麥斯威爾模型方程式中的 τ1g、τ2g、...、τ8g) |
| 容積鬆弛模數 (1 到 8) |
| 時間值 (容積鬆弛模數 1 到 8) (表示廣義麥斯威爾模型方程式中的 τ1k、τ2k、...、τ8k) |
| WLF 方程式參數
|
玻璃轉折溫度 (表示 WLF 方程式中的 T0)
|
| Williams-Landel-Ferry 公式的第一常數 (表示 WLF 方程式中的 C1)
|
| Williams-Landel-Ferry 公式的第二常數 (表示 WLF 方程式中的 C2)
|
當在表格 & 曲線標籤之下定義剪力或容積鬆弛曲線時,曲線的第一個點是在時間 t1 上的 G1 或 K1。在時間 t = 0 時,程式會根據彈性模數及 Poisson 比自動計算 G0 或 K0。
黏彈性材質模型可應用於粗略及精細品質的實體及厚殼元素。
當您使用黏彈性材質模型時,時間在非線性分析中有實際值。