Puede predecir el daño y vida útil restante de una pieza expuesta a cargas cíclicas repetidas con una determinada frecuencia en funcionamiento o a un entorno de vibración aleatoria.
Disponible para SOLIDWORKS Simulation Premium.
Puede realizar un análisis de fatiga según sucesos de dominio de frecuencia que utilizan los resultados de estudios armónicos dinámicos lineales y dinámicos de vibración aleatoria.
La salida de los estudios de fatiga según sucesos de dominio de frecuencia incluye los trazados de vida útil restante y de daños. Para estudios de fatiga basados en vibración aleatoria, también se incluye un trazado de tiempo hasta el fallo.
Fatiga basada en resultados armónicos
Un estudio de fatiga basado en resultados de tensiones como una función de frecuencia de un estudio armónico dinámico lineal, predice la vida útil restante y los daños de una pieza sometida a vibración periódica (o sinusoidal) de un determinado número de ciclos con una determinada frecuencia en funcionamiento.
El cálculo de la relación de daños acumulados se basa en la regla de daño lineal o regla de Miner:
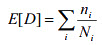
donde E [D] es la relación de daños esperados, nI es el número de ciclos en los que la pieza está sometida a una determinada frecuencia en funcionamiento y la tensión alterna SI y NI es el número de ciclos necesarios para causar fallo en el nivel de tensión SI determinado por la curva S-N del material.
Fatiga basada en resultados de vibración aleatoria
Para calcular el ciclo de fatiga cuando los historiales de tensión o deformación unitaria obtenidos de la estructura o componente son aleatorios por naturaleza (y, por lo tanto, se describen mejor mediante parámetros estadísticos como funciones de densidad de probabilidad, cruces cero hacia arriba y número de picos por segundo), están disponibles estos métodos de cálculo de dominio de frecuencia:
- Banda estrecha
- Steinberg
- Wirsching
La suposición de predicción de ciclo de fatiga basada en frecuencia es que los parámetros de respuesta (tensión y deformación unitaria) del modelo analizado son aleatorios, estacionarios y gausianos por naturaleza.
A diferencia de otros estudios de fatiga, la curva S-N de material se define mediante la ecuación de Basquin:
N = B / (Se)m
donde N = número permitido de ciclos hasta fallo; B = constante específica de la curva (entrecruzamiento del eje S); Se = intervalo de tensión de carga cíclica; m = pendiente de la curva S-N linear.
Esta ecuación muestra que con una carga cíclica de amplitud constante, existe una relación lineal entre ciclos hasta fallo N y el intervalo de tensión Se aplicado cuando se traza en una escala Log-Log.