Für zufällige Vibrationsstudien werden die folgenden Integrationsmethoden verwendet.
Standardmethode
Bei der Standardmethode für zufällige Vibrationsanalysen wird die folgende Vorgehensweise verwendet:
-
Um jede abgefragte Eigenschwingung werden bestimmte Frequenzpunkte ausgewählt. Die Positionen dieser Punkte hängen vom Wert des Einflussparameters "p" ab.
Bei einem Einflussparameter gleich 1,0 sind alle Frequenzpunkte gleichförmig zwischen den Eigenfrequenzen verteilt. Bei einem Einflussparameter größer als 1,0 werden die Punkte im engeren Abstand zu den Eigenfrequenzen gewählt. Die Standardwerte für die Frequenzpunkte und den Einflussparameter werden als Funktion von ζ (Dämpfungsverhältnis der 1. Schwingung) angegeben. Eine Abbildung zur Auswahl der Frequenzpunkte finden Sie hier.
Nachstehend sind die Standardwerte für die Frequenzpunkte und den Einflussparameter als Funktion von ζ angegeben:
| Modales Dämpfungsverhältnis
|
Anzahl der Frequenzen (Standard)
|
Einflussparameter (Standard)
|
|---|
| ζ < 0,01
|
21 |
11
|
| 0,01 < ζ < 0,1 |
21-4,34 Zoll (ζ/0,01)
|
11-3,47 Zoll (ζ/0,01)
|
| ζ < 0,1
|
11
|
3
|
Die Software wendet die in Tabelle 1 angegebenen Standardwerte an, wenn sowohl für die Anzahl der Frequenzpunkte als auch den Einflussparameter der Wert Null (0) definiert ist.
- Die modale Reaktion der spektralen Leistungsdichte wird an jedem Frequenzpunkt bewertet. Das Kreuzmodus-Grenzverhältnis (Verhältnis) fungiert als Grenzwert für das Verhältnis aller möglichen Eigenfrequenzpaare (wi / wj, i > j).
Das bedeutet, dass bei jedem Schwingungspaar mit dem Wert wi / wj > Verhältnis die kreuzspektralen Dichtekomponenten vernachlässigt werden. Wenn Verhältnis = 1 ist, werden die Kreuzmoduseffekte nicht berücksichtigt.
- Die modale Reaktion der spektralen Leistungsdichte wird dann über den angegebenen Frequenzbereich numerisch integriert, um die quadratischen Mittelwerte und Kovarianzen der modalen Reaktion zu ermitteln. Die Integration erfolgt numerisch auf Basis einer Log-Log-Interpolation mittels der Gauß-Integrationsordnung 2 oder 3 über jedes Frequenzintervall. Die quadratischen Reaktionsmittelwerte werden durch Summierung der Intervallwerte ermittelt.
- Schließlich ergeben sich durch die Umwandlung der Schwingungs- zu Knotenkoordinaten die quadratischen Mittelwerte von Verschiebungen, Geschwindigkeiten und Beschleunigungen des Systems.
Näherungsmethode
Die Standardintegrationsmethode kann aufgrund der numerischen Integration großer Matrizen in Bezug auf den Rechenaufwand sehr zeitintensiv sein. Für die Integration bietet die Näherungsmethode eine vereinfachte Lösung, indem sie von folgenden Annahmen ausgeht:
- Die Kreuzmodusreaktion Sx(ω), d. h. die Auswirkung einer Schwingung auf eine andere, wird vernachlässigt. Das bedeutet Folgendes:
(Gleichung 1)
- Die spektrale Leistungsdichte der Erregungen wird um jede Schwingung als konstant angenommen. Daher wird ebenfalls vorausgesetzt, dass jede Schwingung durch "weißes Rauschen" mit der spektralen Dichte Sn erregt wird. Dabei gilt Folgendes:
(Gleichung 2)
ωn ist die Eigenfrequenz der Schwingung n (n = 1,2,...nf).
Bei weißem Rauschen können die quadratischen Reaktionsmittelwerte analytisch für die modalen Reaktionen bestimmt werden:
(Gleichung 3)
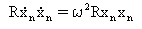(Gleichung 4)
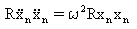(Gleichung 5).