Il sistema di equazioni del movimento di un sistema lineare di n gradi di mobilità ingrandito da una forza variante è:
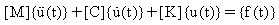 (Equazione 1)
(Equazione 1)
dove:
[M] = n x n matrice di inerzia simmetrica
[C] = n x n matrice di smorzamento simmetrico
[K] = n x n matrice di rigidezza simmetrica
{f(t)} = n-vettore di forza di quotatura
{u},  e
e  sono rispettivamente i vettori n di quotatura di spostamento, velocità e accelerazione.
sono rispettivamente i vettori n di quotatura di spostamento, velocità e accelerazione.
(Equazione 1) è un sistema di n equazioni differenziali ordinarie simultanee con coefficienti costanti. Le equazioni del movimento sono accoppiate mediante termini di massa, rigidezza e smorzamento. L'accoppiamento dipende dal sistema di coordinate usato per descrivere le equazioni del movimento matematicamente.
L'idea fondamentale dietro l'analisi modale è di trasformare il sistema accoppiato di (Equazione 1) in un gruppo di equazioni indipendenti usando la matrice modale [Φ] come matrice di trasformazione. [Φ] contiene le modalità normali {f}i per i = 1, ..., n sistemate così:
 (Equazione 2)
(Equazione 2)
Le modalità normali e i valori eigen del sistema derivano dalla soluzione del problema eigenvalue:
 (Equazione 3)
(Equazione 3)
dove [w2] è una matrice diagonale delle frequenze naturali quadrate.
Per i sistemi lineari, il sistema di n equazioni del movimento possono essere dissociate in n equazioni di grado singolo di mobilità in termini di vettore dello spostamento modale {x}:
 (Equazione 4)
(Equazione 4)
Sostituzione del vettore {u} da (Eq.4) e pre moltiplicandolo per [Φ]T (Equazione 1) genera:
 (Equazione 5)
(Equazione 5)
Le modalità normali soddisfano la proprietà ortogonale e la matrice modale [Φ] viene normalizzata per soddisfare le seguenti equazioni:
 (Equazione 6)
(Equazione 6)
 (Equazione 7) e
(Equazione 7) e
 (Equazione 8).
(Equazione 8).
Sostituendo (Equazioni.6--8), (Equazione 5) diviene un sistema di n equazioni differenziali di secondo ordine SDOF indipendenti:
 per i =1, ..., n (Equazione 9)
per i =1, ..., n (Equazione 9)
(Equazione 9) viene risolta usando i metodi di integrazione passo per passo come Wilson-Theta e Newmark.
L'integrazione viene effettuata nel dominio temporale, dove i risultati dell'ultima fase sono utilizzati per prevedere quelli della successiva.
Il vettore di spostamento del sistema (u) è derivato da (Equazione 4).