Materiały sprężyste posiadające zdolności rozpraszania energii mechanicznej dzięki zjawiskom wiskotycznym są charakteryzowane jako materiały wiskoelastyczne.
W stanach naprężeń wieloosiowych, relację konstytucyjną można zapisać jako:

gdzie: e(bar) i φ są odkształceniami dewiatoryjnymi i wolumetrycznymi, a G(t - τ) i K(t - τ) są funkcjami relaksacji objętościowej i ścinania.
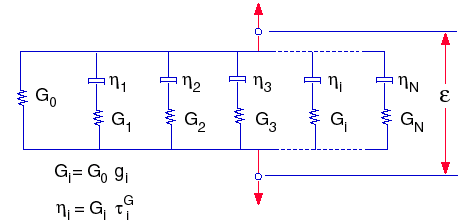
Funkcje relaksacji można następnie przedstawić w modelu mechanicznym, który zwykle określa się jako uogólniony model Maxwella o równaniach:

gdzie: G0 = E / 2(1+ ν), początkowy współczynnik sprężystości poprzecznej (t = 0)
oraz K0 = E / 3(1 -2ν), początkowy współczynnik objętościowy (t = 0)
gi, ki, τi
G i τi
K są i-tymi modułami ścinania i objętościowymi oraz odpowiednimi czasami.
Wpływ temperatury na zachowanie materiału jest uwzględniany poprzez użycie zasady zależności czasowo-temperaturowej. Postać matematyczna zasady:

γt jest czasem zredukowanym, a γ jest funkcją przesunięcia. Jako przybliżenie tej funkcji używane jest równanie WLF (Williams-Landel-Ferry):

gdzie T0 jest temperaturą odniesienia, która jest zwykle wybierana jako temperatura zeszklenia; C1 i C2 są stałymi zależnymi od materiału.
| Parametr |
Właściwość materiału |
|---|
| Parametry liniowe sprężyste |
Współczynnik sprężystości wzdłużnej w X
|
|
Współczynnik Poissona w XY
|
|
Współczynnik sprężystości poprzecznej w XY
|
| Parametry funkcji relaksacyjnej |
Moduł relaksacji ścinania (1 do 8) (reprezentują g1, g2, ..., g8 w równaniach uogólnionego modelu Maxwella)
|
|
Wartości czasu (moduł relaksacji ścinania 1 do 8) (reprezentują moduły τ1
g, τ2
g, ..., τ8
g w równaniach uogólnionego modelu Maxwella) |
|
Moduł relaksacji sprężystości objętościowej (1 do 8) |
|
Wartości czasu (moduł relaksacji sprężystości objętościowej 1 do 8) (reprezentują moduły τ1
k, τ2
k, ..., τ8
k w równaniach uogólnionego modelu Maxwella) |
| Parametry równania WLF
|
Temperatura przejścia szklistego
(reprezentuje T0 w równaniu WLF)
|
|
Pierwsza stała dla równania Williams-Landel-Ferry
(reprezentuje C1 w równaniu WLF)
|
|
Druga stała dla równania Williams-Landel-Ferry
(reprezentuje C2 w równaniu WLF)
|
Podczas definiowania krzywej relaksacyjnej ścinania lub objętościowej na karcie Tabele i krzywe pierwszym punktem krzywej jest moduł G1 lub K1 o czasie t1. W czasie t = 0 program automatycznie oblicza G0 lub K0 na podstawie współczynnika sprężystości wzdłużnej i współczynnika Poissona.
Wiskoelastyczny model materiału może być używany z elementami grubej skorupy lub bryłowymi jakości roboczej i wysokiej.
Czas ma wartość rzeczywistą w analizie nieliniowej przy użyciu modelu materiału lepkoelastycznego.