A matriz simétrica n x n do amortecimento [C] é formulada como a combinação linear das matrizes da massa [M] e da rigidez [K]:
(Equação 1)
-
Coeficiente Alpha: Define o coeficiente de massa proporcional α.
-
Coeficiente Beta:Define o coeficiente de rigidez proporcional β.
O tipo de amortecimento descrito pela (Equação 1) é conhecido como Rayleigh, ou amortecimento proporcional.
Esta forma de [C] é ortogonal em relação aos autovetores do sistema.
Aplicando a transformação de coordenadas modal, a matriz de amortecimento modal [c] se torna diagonal:
(Equação 2)
Você pode definir o amortecimento de Rayleigh para estudos dinâmicos lineares e não lineares.
Relação entre coeficientes de Rayleigh e razão de amortecimento modal
A matriz de amortecimento modal [c] é dada por:
(Equação 3)
O coeficiente de amortecimento viscoso ci para o i-ésimo modo é calculado por:
(Equação 4),
e a razão de amortecimento viscoso ζi é expressa como
(Equação 5)
Se as razões de amortecimento para os modos i-ésimo e j-ésimo são ζi e ζj, então os coeficientes de Rayleigh a e b são calculados a partir da solução das duas equações algébricas:
(Equação 6)
Se ambos os modos têm a mesma razão de amortecimento ( ζi = ζj = ζ), então os valores de α e β são dados por:
(Equação 7) 
(Equação 8)
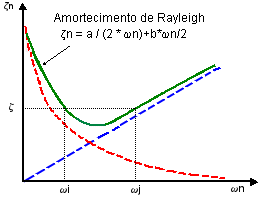
A razão de amortecimento viscoso ζ para qualquer outro modo varia com a frequência, como mostrado na figura:
