A partir de una curva S-N de resistencia a la fatiga de un material determinado, puede derivar las constantes de la ecuación de Basquin o bien dejar que el programa calcule dichas constantes especificando el número de puntos de datos en la curva de S-N que incluir en los cálculos de ajuste de curva.
Algunos materiales disponibles de la base de datos de materiales de SOLIDWORKS y el portal web de materiales de SOLIDWORKS tienen información de datos curva S-N de fatiga. Por ejemplo, la curva S-N del material Ti-6AI-4V (aleación de Metal_Ti Alpha-Beta) descargada del portal web de materiales de SOLIDWORKS (el formato de la base de datos de materiales es *.sldmat) se muestra en una escala log S - log N.
Los valores numéricos de los primeros cuatro puntos de datos de S-N se expresan en la tabla.

La ecuación de Basquin es una relación de ley de potencia que describe la relación lineal entre los ciclos de tensión aplicados (S) en el eje Y y el número de ciclos hasta fallo en el eje X trazada en una escala Log-Log.
Puede definirse como:
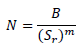
donde N es el número de ciclos hasta el fallo (normalmente más de 104), Sr es el valor de referencia de resistencia a la fatiga (en Simulation este es el intervalo de tensión que se toma como 2* tensión alterna), m es la pendiente de la curva de fatiga log S - log N y B es el valor de la tensión en un ciclo.
Para calcular la pendiente m de la ecuación de Basquin, resuelva el sistema de ecuaciones:
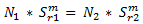
Para resolver m, tome el registro de ambas expresiones:
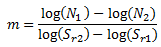
Mediante la sustitución de los dos primeros puntos de datos de S-N de la tabla anterior, calcule primero m y, a continuación, B:
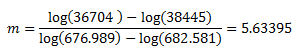

Para la constante B, el programa tiene en cuenta el valor de intervalo de tensión (desde la tensión cíclica máxima a la tensión cíclica mínima). Si los valores de tensión de la curva S-N se proporcionan como tensiones alternas (que es la práctica común), multiplique estas tensiones por 2 para calcular la constante B (intervalo de tensión = 2* tensión alterna, suponiendo una tensión media de cero e inversión completa de la carga cíclica). Si los datos de la curva S-N se expresan en valores de intervalo de tensión, aplíquelos directamente en la ecuación para calcular la constante B. Para el cálculo de la constante de pendiente m, la multiplicación de las tensiones no se altera el valor de pendiente.
En la pestaña
Curvas SN de fatiga (cuadro de diálogo
Material) introduzca los valores de B en
Constante específica de la curva (B) y m en
Pendiente de la curva S-N (m). Seleccione las unidades de tensión adecuadas en
Unidades y borre
Constantes de Basquin estimadas para la curva S-N.
También puede buscar los trazados de curvas de resistencia a la fatiga en los códigos como el Eurocódigo 9: Proyecto de estructuras de aluminio: Estructuras susceptibles a la fatiga, Ref. EN 1999-1-3:2007/A1.
Ejemplo de curva S-N de resistencia a la fatiga
En el Eurocódigo 9 puede encontrar valores numéricos para la pendiente constante m para diferentes categorías de detalle y, a continuación, calcular B.
Por ejemplo, en la Tabla de referencia J.2: Categorías de detalle para miembros planos, EN 1999-1-3:2007/A1 para una chapa simple con taladros, el intervalo de tensión DS = 100 MPa en n = 2x106 ciclos y la pendiente M = 7; y B igual a:
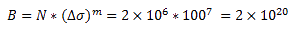
Para dejar que el programa realice el ajuste de curva en un determinado conjunto de datos S-N a una línea recta, seleccione Constantes de Basquin estimadas para la curva S-N. En este caso, asegúrese de que Interpolar está configurado en Log-log y seleccione el último punto de datos de S-N que tener en cuenta para el ajuste de curva en Tener en cuenta el punto de corte de la curva S-N en la fila.
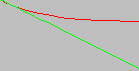
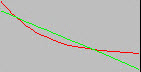
Los dos gráficos muestran la superposición de una curva S-N original (línea roja) con la línea de ajuste de curva de la ecuación Basquin (línea verde) para 2 (a) y 22 (b) puntos de datos de S-N respectivamente. Se recomienda comprobar la calidad del ajuste de curva de Basquin antes de continuar con el análisis. La calidad de la línea de ajuste de curva al aproximarse a la curva S-N original es mejor para la parte de la curva S-N hasta el punto de corte.
|
|
| (a) Ajuste de curva de Basquin con 2 puntos de datos de S-N (línea verde). |
(b) Ajuste de curva de Basquin con 22 puntos de datos de S-N (línea verde). |