この基準は降伏状態において、媒体の全ての点における最大せん断応力が同じで、与えられた材料の単軸張力試験から得られた降伏応力の半分であるとの仮定に基づいています。
3次元の事例で、最低1つの不等状態が満たされると降伏が生じます:
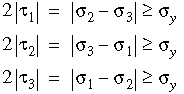
つまり、降伏は最大主応力と最小主応力との間の差の半分に等しい最大せん断応力に基づいています。したがって、この基準において中間主応力は降伏状態に影響しません。
一部のデザイン コードと参照では、Tresca 相当応力は、(σ1 – σ3)または応力密度と等しい最大せん断応力の 2 倍に定義されます。
せん断応力強さ(Shearing Stress Intensity)
せん断応力強さは、応力偏差値の第2不変式の平方根により定義され、次のように表されます:

純せん断状態(State of Pure Shear)
純せん断状態は、次のように定義されます:

この状態では、せん断応力強さおよび最大せん断応力は同等です:

Tresca 条件を使用した降伏点でのせん断応力は、引張り降伏応力の半分として取得されます:

von Mises 降伏基準に基づくせん断降伏応力は次に相当します:

- Tresca モデルでは、等方性および運動学的硬化則のどちらも使用できます。等方性あるいは運動学硬化則の線形の組み合わせは、偏差空間の半径と降伏サーフェスの両方が、荷重の履歴に関して変化することができるとき、設定されます。
-
硬化係数は等方硬化性および運動学的硬化則の大きさを定義します。
- 純等方硬化性では硬化係数は値 0 を持ちます。降伏サーフェスの半径は拡大されますが、その中心は偏差空間で固定されたままです。
- 純移動硬化則では、硬化係数は値 1 を持ちます。降伏サーフェスの半径は、その中心は偏差空間で移動される間、一定に保たれます。