Os seguintes métodos de integração são usados em estudos de vibração aleatória:
Método padrão
O método padrão para análise de vibração aleatória é realizado da seguinte maneira:
-
Determinados pontos de frequência são selecionados em torno de cada modo natural solicitado. A localização desses pontos depende do valor do parâmetro de tendência p.
O parâmetro de tendência 1,0 indica que todos os pontos de frequência estão uniformemente distribuídos entre as frequências naturais. Se o parâmetro de tendência for maior do que 1,0, os pontos estão selecionados mais próximos das frequências naturais. Os valores padrão para os pontos de frequência e o parâmetro de tendência são dados como uma função da razão de amortecimento ζ do primeiro modo. Para ver uma ilustração na seleção dos pontos de frequência, clique aqui.
Os valores predeterminados dos pontos de frequência e do parâmetro de tendência como uma função de ζ são mostrados abaixo:
| Razão de amortecimento modal |
Número de frequências (predeterminado) |
Parâmetros de tendência (predeterminado) |
|---|
| ζ < 0,01 |
21 |
11 |
| 0,01 < ζ < 0,1 |
21-4.34 ln(ζ /0,01) |
11-3,47 ln(ζ /0,01) |
| ζ < 0,1 |
11 |
3 |
O software aplica os valores padrão apresentados na Tabela 1 quando zero (0) é definido para o Número de pontos de frequência e para o Parâmetro de tendência.
-
PSDs modais de resposta são avaliadas em cada ponto de frequência. A razão de corte do modo cruzado (RAZÃO) define um limite na razão de todos os pares de frequências naturais possíveis (wi / wj, i > j).
Isso significa que, para cada par de modos com wi / wj > RAZÃO, os termos de densidade de espectro cruzado são desprezados. Os efeitos de modo cruzado não são considerados para RAZÃO = 1.
- As PSDs modais são então integradas numericamente no intervalo de frequência especificado para fornecer os valores médios quadráticos e as covariâncias da resposta modal. A integração é efetuada numericamente utilizando a integração de Gauss de ordem 2 ou 3 em cada intervalo de frequência, com base em uma interpolação log-log. A resposta média quadrática é obtida somando as contribuições do intervalo.
- Finalmente, a transformação de modal para nodal fornece deslocamentos, velocidades e acelerações rms do sistema.
Método aproximado
O método padrão de integração pode ser demorado devido à integração numérica de grandes matrizes. O método aproximado de integração obtém uma solução simplificada ao estabelecer as seguintes suposições:
-
Desprezar a resposta de modo cruzado, Sx(ω), que é o efeito de um modo sobre o outro, ou seja,
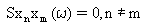 (Equação 1)
(Equação 1)
-
As PSDs de excitações são consideradas constantes em torno de cada modo. Assim, pressupõe-se que cada modo seja excitado por "ruído branco" com densidade espectral Sn, onde;
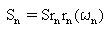 (Equação 2)
(Equação 2)
ωn é a frequência natural do modo n (n = 1,2,...nf).
Para o ruído branco, as respostas médias quadráticas podem ser determinadas analiticamente para as respostas modais:
 (Equação 3)
(Equação 3)
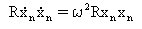 (Equação 4)
(Equação 4)
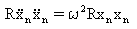 (Equação 5)
(Equação 5)