As forças internas em um corpo variam de um ponto a outro. Em qualquer área de plano interno, a parte do corpo localizada em um lado da área exerce cargas na área localizada no outro lado. A tensão denota a intensidade dessas forças internas (força por unidade de área).
Tensão
Em um corpo contínuo, é possível calcular a tensão em um ponto
- Imagine um plano arbitrário que corta o corpo naquele ponto,
- Considere uma área infinitamente pequena DA ao redor do ponto no plano,
- Supondo que a magnitude da força transmitida através do ΔA em uma certa direção seja ΔF,
- A tensão naquela direção será expressa por ΔF/ΔA em que ΔA aproxima-se de 0.
a definição acima é de um vetor de tensão ou tração em um ponto. O vetor de tração não define com exclusividade o estado da tensão em um ponto. Ele varia dependendo do plano arbitrário escolhido. Um tensor de tensão, por exemplo o tensor de tensão verdadeiro, definido como σ = n.T(multiplicação da matriz), onde n é o vetor normal associado ao plano e T é o vetor de tensão ou de tração, define a tensão de maneira única.
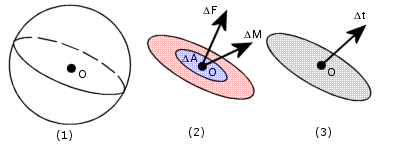
Figura (1): Um plano passa pelo ponto O, dividindo o corpo em duas partes.
Figura (2): Força resultante e vetores de movimento em uma região de área DA ao redor do ponto O no plano.
Figura (3): O vetor de limite de tensão no ponto O do plano.
Deformação
A deformação é a razão da alteração no comprimento em δL ao comprimento original L. A deformação é uma quantidade sem dimensão.
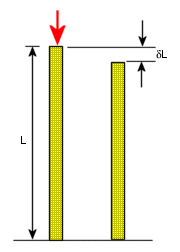
Deformação = δL/L
Sequência de cálculos
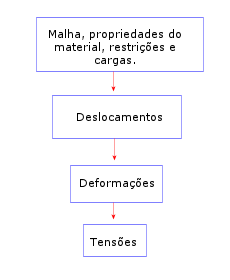
Dado um modelo em malha com um conjunto de cargas e restrições de deslocamento, o programa de análise estática linear procede da seguinte forma:
- O programa constrói e resolve um sistema de equações lineares de equilíbrio de elementos simultâneos finitos para calcular os componentes de deslocamento em cada nó.
- O programa então usa os resultados de deslocamento para calcular os componentes de deformação.
- O programa usa os resultados de deformação e as relações tensão-deformação para calcular as tensões.
Cálculos de tensão
Resultados de tensão são primeiramente calculados em pontos especiais, chamados de pontos gaussianos ou pontos de quadratura, localizados dentro de cada um dos elementos. Estes pontos são selecionados para a obtenção de resultados numéricos excepcionais. O programa calcula as tensões nos nós de cada elemento através da extrapolação dos resultados disponíveis nos pontos gaussianos.
Após uma execução bem-sucedida, os resultados de tensão dos nós, para todos os nós de todos os elementos, estarão disponíveis no banco de dados. Nós comuns a dois ou mais elementos possuem múltiplos resultados. Em geral, esses resultados não são idênticos porque o método de elementos finitos é um método de aproximação. Por exemplo, se um nó for comum a três elementos, pode haver três valores ligeiramente diferentes para cada componente de tensão do nó.
Ao exibir os resultados de tensão, é possível pedir a tensão de elementos ou nós. Para calcular as tensões dos elementos, o programa calcula a média das tensões dos nós de cada elemento. Para calcular as tensões dos nós, o programa calcula a média dos resultados correspondentes de todos os elementos que compartilham determinado nó.