Для выполнения нелинейного анализа были придуманы различные методы управления. Настоящие методы могут быть классифицированы как:
Метод управления с приращениями нагрузки
В настоящей концепции нагрузки, приложенные к системе, используются как заданные переменные. Каждое состояние (точка) на равновесной траектории определяется пересечением поверхности (F = константе) с траекторией для определения параметров деформации.

В адаптации настоящего метода для расчета методом конечных элементов, нагрузки (передвижения основания, заданные перемещения, термические, сила тяжести, и т. п.) прикладываются по нарастающей, как задано ассоциированными кривыми “времени”.
Инкрементный метод управления перемещением
В настоящем методе точка на равновесной траектории определяется пересечением с поверхностью, определенной постоянным параметром деформации (U = константе), с кривой решения, как показано на рисунке ниже.
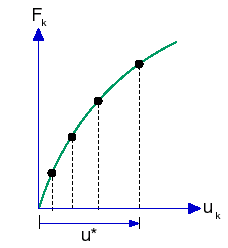
Чтобы внедрить настоящий метод в анализ конечных элементов, массив приложенных нагрузок пропорционально прирастает (используя множитель сосредоточенной нагрузки) для достижения равновесия под контролем заданных степеней свободы (DOF). Управляемые степени свободы, заданные посредством выбора вершины или справочной точки, возрастают, используя кривую “времени”.
Инкрементный метод управления длиной дуги
В настоящей концепции задан специальный параметр посредством ограничения (вспомогательного) уравнения, которое добавлено к системе уравнений, управляющих равновесием системы. В геометрическом смысле, регулируемый параметр можно просматривать в виде “длины дуги” равновесной траектории, как показано на рисунке ниже.
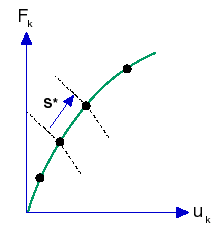
Чтобы использовать метод. в анализе конечных элементов, массив приложенных нагрузок пропорционально прирастает (используя множитель сосредоточенной нагрузки) для достижения равновесия под контролем заданной длины (длины дуги) равновесной траектории. Длина дуги будет автоматически вычисляться программой. Не требуется кривой “времени”.
Как управление силой, так и управление перемещением будут прерываться в окрестности критических точек (называемых потерей устойчивости для контроля усилия и восстановлением устойчивости для управления перемещением), как на этом рисунке. Эти трудности обычно встречаются при анализе потери устойчивости рам, колец и оболочек. Управление длиной дуги успешно преодолевает эти трудности.
