Le système d'équations de mouvement d'un système linéaire à n degrés de liberté excité par une force variable dans le temps est:
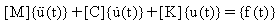(Equation 1)
En utilisant la transformation des coordonnées, l'ensemble de n équations simultanées se réduit à n équations indépendantes (chaque équation pouvant être résolue indépendamment) :
pour r = 1, 2, ...., n (Equation 2)
où xr(t) sont les coordonnées modales reliées aux coordonnées des nœuds ur(t) par:
(Equation 3).
Le vecteur des chargements modaux {m(t)} est donné par :
(Equation 4).
En supposant que les excitations sont exprimées par leurs fonctions de densité spectrale de puissance (PSD), la solution peut être exprimée par la représentation en fréquences. Si la matrice de densité spectrale de puissance (PSD) d'excitation est exprimée sous la forme [Sf(ω)], la matrice de densité spectrale de puissance (PSD) de la force modale est définie comme :
(Equation 5).
La densité spectrale de puissance (PSD) de la réponse de déplacement modal [Sx(ω)] est obtenue à partir de :
(Equation 6),
où [H(ω)] est la matrice de fonction de transfert modal et [H*(ω)] est son nombre complexe conjugué. Dans le cas des modes normaux, la matrice de fonction de transfert est diagonale par rapport aux éléments diagonaux Hr(ω)
(Equation 7) et
(Equation 8).
La densité spectrale de puissance de la réponse de déplacement [Su(ω)] est alors dérivée de (Equation 3).
(Equation 9).
La densité spectrale de puissance des réponses de vitesse et d'accélération est exprimée par:
(Equation 10) et
(Equation 11).
Les densités spectrales de puissance de vitesse et d'accélération sont reliées à la densité spectrale de puissance de déplacement modal par:
(Equation 12) et 
(Equation 13)
Equation 10 et Equation 11 peuvent être écrites de nouveau sous la forme :
(Equation 14) et
(Equation 15).
Les réponses d'auto-corrélation modale à retard nul (τ=0) en termes de la densité spectrale de puissance (PSD) de la réponse modale sont calculées à partir des intégrales :
(Equation 16)
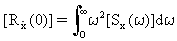(Equation 17)
(Equation 18).
Pour les équations ci-dessus, les réponses de moyenne quadratique sont déterminées à partir des termes diagonaux des matrices:
(Equation 19),
(Equation 20),
(Equation 21).
Réponse de moyenne quadratique de contrainte
Les éléments de contrainte {σ} sont déterminés à partir des déplacements de nœuds {u} par :
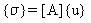(Equation 22) ou, en termes de déplacements modaux {x} par :
(Equation 23), où [Φ] est la matrice de vecteurs propres.
La matrice de corrélation de contrainte [Rσ] est donnée par :
(Equation 24).