시간 변위 하중으로 자극을 받은 선형 n 자유도 시스템의 모션 수식 시스템:
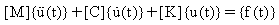 (수식 1)
(수식 1)
좌표 이동을 사용하면, n 연립 방정식 세트가 n 독립 수식(즉, 각 수식을 별도로 풉니다)으로 분리됩니다.
 r = 1, 2, ...., n (수식 2)
r = 1, 2, ...., n (수식 2)
여기서, xr(t)은 노드 좌표 ur(t)와 다음 상응 수식의 모달 좌표계임:
 (수식 3).
(수식 3).
주어진 모달 하중 {m(t)} 벡터:
 (수식 4).
(수식 4).
여진이 PSD (Power Spectral Density) 함수로 표현된다고 가정할 때, 이론해는 진동수 영역으로 수식화됩니다. 여진 psd 매트릭스가 [Sf(ω)]일 때, 정의되는 모달 하중 psd 매트릭스:
 (수식 5).
(수식 5).
모달 변위 응답 [Sx(ω)]의 PSD는 다음에서 얻어집니다.
 (수식 6),
(수식 6),
여기서 [H(ω)]는 모달 전이 함수 매트릭스이며, [H*(ω)]는 복소수 공액입니다. 정상 모드의 경우, 전이 함수 매트릭스는 대각 요소 Hr(ω)와 대각을 이룹니다.
 (수식 7), 그리고
(수식 7), 그리고
 (수식 8).
(수식 8).
변위 응답 psd [Su(ω)]는 (수식 3)에서 얻어집니다.
 (수식 9).
(수식 9).
속도와 가속도 응답의 PSD 수식:
 (수식 10), 그리고
(수식 10), 그리고
 (수식 11).
(수식 11).
모달 속도와 가속도 PSD는 다음 수식에 의해 모달 변위 PSD에 연관됩니다.
 (수식 12),
(수식 12),  (수식 13)
(수식 13)
수식 10과 수식 11을 다음과 같이 다시 작성할 수 있습니다.
 (수식 14)과
(수식 14)과  (수식 15).
(수식 15).
모달 응답 PSD 관점에서 0 딜레이 모달 자동 상관 응답(τ=0)는 적분법으로 계산됩니다.
 (수식 16)
(수식 16)
 (수식 17)
(수식 17)
 (수식 18).
(수식 18).
위 수식에서, 평균 제곱 응답은 매트릭스의 대각으로 정해집니다.
 (수식 19),
(수식 19),
 (수식 20),
(수식 20),
 (수식 21).
(수식 21).
응력 평균 제곱 응답
요소 응력 {σ}는 노달 변위 {u}에서 다음 수식으로 결정됩니다.
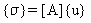 (수식 22), 또는 모달 변위{x} 관점에서 다음과 같은 수식:
(수식 22), 또는 모달 변위{x} 관점에서 다음과 같은 수식:
 (수식 23), 여기서 [Φ]는 고유 벡터 매트릭스입니다.
(수식 23), 여기서 [Φ]는 고유 벡터 매트릭스입니다.
상응 응력 매트릭스 [Rσ] 수식:
 (수식 24).
(수식 24).