Los materiales elásticos que tienen la capacidad de disipar la energía mecánica debido a efectos viscosos se caracterizan como materiales viscoelásticos.
Para un estado de tensión multiaxial, la relación constitutiva puede formularse de la siguiente manera:

donde: e(bar) y φ son las deformaciones unitarias desviatorias y volumétricas, G(t - τ) y K(t - τ) son funciones de relajación cortantes y de compresibilidad.
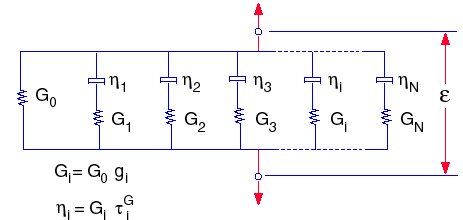
Las funciones de relajación pueden representarse mediante el modelo mecánico, normalmente denominado Modelo de Maxwell generalizado, que tiene las siguientes expresiones:

donde: G0 = E / 2(1+ v), módulo cortante inicial (t=0)
y K0= E / 3(1 -2v), módulo de masa inicial (t=0)
gi, ki, τi
G y τi
K son los módulos cortantes y de comprensibilidad i-avo y los tiempos correspondientes.
El efecto de la temperatura en el comportamiento del material se presenta mediante el principio de correspondencia entre tiempo-temperatura. La forma matemática del principio es:

donde γt es el tiempo reducido y γ es la función de cambio. La ecuación WLF (Williams-Landel-Ferry) se utiliza para realizar una aproximación de la función:

donde T0 es la temperatura de referencia que generalmente se selecciona como la Temperatura de transición vítrea; C1 y C2 son constantes dependientes del material.
| Parámetro |
propiedad de material |
|---|
| Parámetros elásticos lineales |
Módulo de elasticidad en x
|
|
Coeficiente de Poisson en xy
|
|
Módulo cortante en xy
|
| Parámetros de función de relajación |
Módulo de relajación cortante (1 a 8) (representan g1, g2,... g8 en las ecuaciones del Modelo de Maxwell generalizado)
|
|
Valores de tiempo (Módulo de relajación cortante de 1 a 8) (representan τ1
g, τ2
g,..., τ8
g en las ecuaciones del Modelo de Maxwell generalizado) |
|
Módulo de compresibilidad (1 a 8) |
|
Valores de tiempo (Módulo de compresión de 1 a 8) (representan τ1
k, τ2
k,..., τ8
k en las ecuaciones del Modelo de Maxwell generalizado) |
| Parámetros de ecuación WLF
|
Temperatura de transición vítrea
(representa T0 en la ecuación WLF)
|
|
Primera constante para la ecuación de Williams-Landel-Ferry
(representa C1 en la ecuación WLF)
|
|
Segunda constante para la ecuación de Williams-Landel-Ferry
(representa C2 en la ecuación WLF)
|
Al definir una curva de relajación cortante o de compresibilidad en la pestaña Tablas y curvas, el primer punto de la curva es el módulo G1 o el módulo K1 en el momento t1. En el momento t = 0, el programa calcula automáticamente G0 o K0 a partir del módulo elástico y el coeficiente de Poisson.
El modelo de material viscoelástico puede utilizarse con los elementos de vaciado sólido y grueso de alta calidad y calidad de borrador.
Tiempo tiene valores reales en el análisis no lineal cuando se utiliza el modelo de material viscoelástico.