大歪み可塑性理論では、対数歪み測度は次のように定義されます。 
ここで Uは一般に変形勾配 F (すなわち、F = R U、R は回転テンソル) の右極分解から取得される右伸張テンソルです。 増分の対数歪みは、次のように予測されます。 
ここで B(n+1/2) は解析ステップ n+1/2 で予測されたひずみ-変位マトリックス、そして Δu は増分変位ベクトルです。 上記は、正しい式に対する 2 番目の近似であることに注意してください。
構成モデルをフレーム不変あるいは客観的にたもつため、応力比率はGreen-Naghdi比率として取得されます。 応力比率を全体座標系から R座標系に変換することにより、
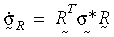
全構成モデルは、小歪み理論と同じ形となります。 大歪み塑性理論は、von Mises 降伏規準、関連フロー規則、等方性または運動学硬化則 (双線形または多線形) に適用されます。 材料特性の温度依存は、双線形硬化によってサポートされています。 この事例では、radial-return アルゴリズムが使用されています。 基本的な概念は、垂直ベクトル N を次により近似化することです:

ここで、
下図は、上の 2 つの等式を図解するものです。

要素力ベクトルおよび剛性マトリックスは、最新の Lagrangian 方程式に基づいて算出されます。 Cauchy 応力、対数歪み、現在の厚み (シェル要素のみ) は出力ファイルに記録されます。
現在の事例の弾性は、弾性の小歪みを仮定するが、プラスチックの大歪みを任意で使用できるようにする超弾性形式でモデル化されています。 ゴムのように弾性の歪みが大きい場合は、Mooney-Rivlin などの超弾性材料モデルを使用できます。
多線形応力-歪み曲線の定義では、Cauchy (真) 応力および対数歪みを使用してください。