L'évaluation des dommages de fatigue pour les composants qui fonctionnent dans un environnement de vibration aléatoire est estimée dans le domaine de fréquence basé sur les propriétés statistiques de la fonction de densité spectrale de puissance de la réponse.
Lorsque des structures ou composants mécaniques sont soumis à une forme de chargement aléatoire, telle qu'une éolienne sous l'effet du vent, une structure Offshore sous l'effet d'une vague, ou un moteur de voiture fonctionnant sur différents profils de surface de routes, les estimations de résistance à la fatigue sont effectuées dans le domaine de fréquence.
Le terme fatigue de vibration (ou fatigue basée sur la fréquence) renvoie à l'estimation de résistance à la fatigue où le chargement et la réponse (contraintes ou déformations historiques) sont des phénomènes aléatoires, et sont donc mieux décrits en utilisant des mesures statistiques telles que la densité spectrale de puissance (PSD).
Les caractéristiques statistiques de PSD de la réponse peuvent être obtenues grâce aux moments de fonction de PSD.
| Caractéristiques Statistiques de la PSD |
Equation |
|---|
| Le moment spectral nth moment spectrale de la PSD de la contrainte S(f) à une fréquence f (dans des unités de Hz). |
 (Eq.1)
|
| Valeur moyenne quadratique pour un processus stationnaire gaussien σ. |
 (Eq.2)
|
| Nombre moyen de croisements nuls vers le haut E[0] pour un exemple typique de 1 seconde. |
 (Eq.3)
|
| Nombre moyen de pics E[0] pour un exemple typique de 1 seconde. |
 (Eq.4)
|
| L'irrégularité facteur γ varie entre 0 et 1. Elle s'approche de 1 lorsque le signal de contrainte approche un phénomène de bande étroite (pour une onde sinusoïdale γ = 1). Elle s'approche de 0 lorsque le signal de contrainte approche un phénomène de bruit blanc. |
 (Eq.5)
ou
 (Eq.6)
|
Les propriétés de fatigue du matériau sont généralement obtenues à partir d'une courbe S-N, qui définit la relation entre l'amplitude de contrainte, S (c'est la variation de contrainte entre la contrainte cyclique maximale dans des conditions de tension et la contrainte cyclique minimale en compression) et la moyenne de cycles requis pour entraîner une rupture, N.
Pour la plupart des problèmes de forts cycles de fatigue (n >= 104 ), la courbe S-N peut être exprimée de façon simplifiée :
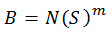(Eq.7)
où B et m sont des propriétés des matériaux variant avec le chargement et conditions d'environnement et sont déterminés par les essais de fatigue.
L'endommagement cumulatif E[AD] en raison de la fatigue due au chargement aléatoire est basé sur la règle de Palmgren-Miner et s'exprime comme suit :
(Eq.8)
où n(S) représente le nombre de cycles appliqués au niveau S d'amplitude de contrainte, p(S) représente la fonction de densité probable de l'amplitude de contrainte. En remplaçant l'équation de la courbe S-N simplifiée dans l'équation ci-dessus, une équation générale d'endommagement de fatigue à partir d'une réponse de contrainte aléatoire est obtenue avec :
(Eq.9), où T est la durée en secondes du chargement aléatoire.
Il existe trois méthodes d'estimation d'endommagement de fatigue basées sur Eq.9 : Méthode Steinberg à trois bandes, méthode bande étroite et méthode Wirshing. Chaque méthode utilise une définition différente pour la fonction de densité probable p(S).
Méthode de bande étroite
Dans la méthode de bande étroite, la fonction de densité probable des pics pour un signal de bande étroite tend vers une distribution Rayleigh (Bendat J.S., Fonctions de probabilité pour réponses aléatoires. Rapport de la NASA sur Contact NASA-5-4590, 1964).
(Eq.10)
En substituant (Eq.10) dans (Eq.9) et en intégrant les résultats à l'expression suivante pour l'estimation d'endommagement de fatigue.
(Eq.11), où Γ(.) est la fonction gamma.
La méthode Wirsching
La méthode Wirsching (Wirshing, P.H., Paez, T.L., et Ortiz K., Vibration aléatoire, John Wiley & Sons Inc., New York, 1995) modifie la méthode de bande étroite avec un facteur de correction empirique pour prendre en compte un phénomène de bande large.
(Eq. 12)
, (Eq. 13)
ζw est un facteur empirique dérivé des simulations Monte-Carlo qui incluent une variété de fonctions de densité spectrale.
αw et bw sont des paramètres mieux adaptés obtenus à partir de :
(Eq. 14)
Méthode Steinberg à trois bandes
L'hypothèse de la méthode Steinberg est que la fonction de densité probable de la réponse de contrainte aléatoire suit une distribution gaussienne, et, par conséquent, les valeurs attendues de la réponse d'amplitudes de contrainte sont limitées par certains niveaux de probabilité :
-
68,27 % de probabilité que l'amplitude des cycles de contrainte ne dépasse pas la plage de 2 fois la moyenne quadratique du signal de réponse de contrainte.
- 27,1 % de probabilité que l'amplitude des cycles de contrainte ne dépasse pas la plage de 4 fois la moyenne quadratique du signal de réponse de contrainte.
- 4,3 % que les cycles de contrainte ne dépassent pas la plage de 6 fois la moyenne quadratique du signal de réponse de contrainte.
Aucun cycles de contrainte ne survient avec les tranches supérieure à 6 fois la moyenne quadratique.
L'endommagement de fatigue attendu est obtenu par :
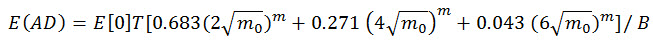(Eq.15)
En simulation, les fonctions de contrainte PSD sont les résultats de l'étude de vibration aléatoire dynamique sur laquelle l'étude de fatigue est basée. Le composant de contrainte de von Mises est pris en compte pour le calcul de l'endommagement attendu en raison de la fatigue pour les trois méthodes.