Discretization Error Estimation

The stress error estimation is based on the principle of the continuity of the stress field. The stress plot ERR: Energy Norm Error provides an estimate of the stress field discontinuity from one element to another.

The nodal stresses of each element are averaged to smooth the discontinuity in the element stresses across the element boundaries. For example, for N elements that share a common node, Simulation sums the stress values from all elements and divides them by N to calculate the averaged stress values at that node. Displacement shape functions (linear or higher-order polynomial) are used to interpolate the new stress field.

The stress error estimate in each element is defined as the difference between the element stress and the average of the nodal stresses corrected using the shape functions. This stress error is used to calculate the energy norm error for each element.

Select the ERR:Energy Norm Error stress component to plot the energy norm error for each element. The ERR:Energy Norm Error plot is only available for static and drop test studies.

The table summarizes the definitions and formulas for the stress error estimates.

Definitions Formulas
Stress error vector

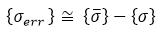
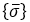  • : average stress vector at a node. If there are N elements that share a common node, the stress values from all N elements are summed and divided by N.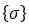
  • : element stress vector at a node (averaged between the Gauss points within each element).
Stress error estimate of element i based on the energy norm

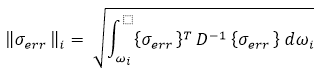
  • D: material stiffness matrix or constitutive matrix
  • w: element volume
Estimate of global stress error (Total Error Energy)

  • N: number of elements
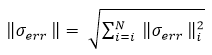
Estimate of elemental percentage error (ERR: Energy Norm Error)

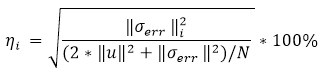
Total strain energy

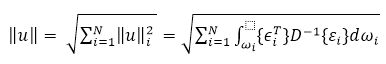
  • : elemental strain vector
Average Percentage Error (APE)
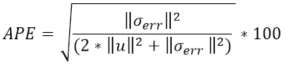  • The output file, *.out, reports the Total Strain Energy (TSE), Total Error Energy (TEE), and Average Percentage Error (APE).
  • If the mesh is fine enough such that two neighboring elements have perfectly continuous stress contours, the stress error at each node would be zero. To reduce the stress error, refine the mesh in areas of high values of energy norm error.

References

  • A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis by O.C. Zienkiewicz and J. Z. Zhu, International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987)
  • An error analysis and mesh adaptation method for shape design of structural components, by K.-H. Chang and . K. Choi (1991), Computers, and Structures Vol. 44. No. 6. pp. 1275-1289, 1992 Pergamon Press Ltd.