Failure Criterion
The Tsai-Hill failure criterion applies to composite shells.
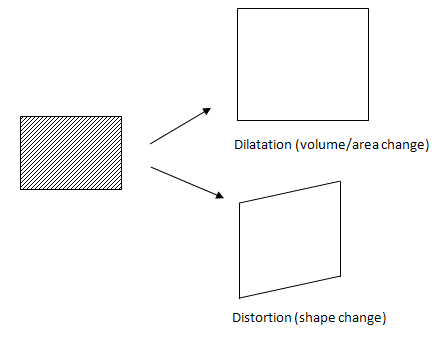
This criterion considers the distortion energy portion of the total strain energy that is stored due to loading. The distortion energy is the portion of strain energy that causes shape change. The other portion is the dilatation energy that causes volume change (area change in the case of 2D) due to loading.
The figure illustrates the difference between dilatation and distortion when a 2D model is loaded.
For a 2D lamina, which is the case for composite shells, each lamina is assumed to be in a state of plane stress with σ3 =0, τ13 =0, τ23 =0. The failure index is computed as follows:
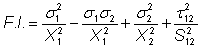
where: X1 is the tensile strength of laminate in material direction 1, X2 is the tensile strength of laminate in material direction 2, and S12 is the shear strength of laminate
See Composite Ply Material Directions for a definition of material directions 1 and 2.
The program reports the factor of safety (FOS) against laminate failure as 1 / Sqrt (F.I.). The FOS is the coefficient by which all stress components should be multiplied to reach laminate failure (F.I. = 1). A FOS value greater than 1 indicates that the laminate is safe from failure.
Further,
X1 = X1T if σ1 > 0
X1 = X1C if σ1 < 0
X2 = X2T if σ2 > 0
X2 = X2C if σ2 < 0
Superscripts T and C denote tensile and compressive strengths respectively.
The Tsai-Hill criterion considers the interaction between different stress components. Hence, it is an interactive failure theory.
Limitation
The Tsai-Hill failure criterion cannot predict different failure modes including fiber failure, matrix failure, and fiber-matrix interface failure.