Since Nitinol is usually used for its ability to undergo finite strains, the large strain theory utilizing logarithmic strains along with the updated Lagrangian formulation is employed for this model.
The constitutive model is, thus, constructed to relate the logarithmic
strains and the Kirchhoff stress components. However, ultimately the constitutive
matrix and the stress vector are both transformed to present the Cauchy (true)
stresses.
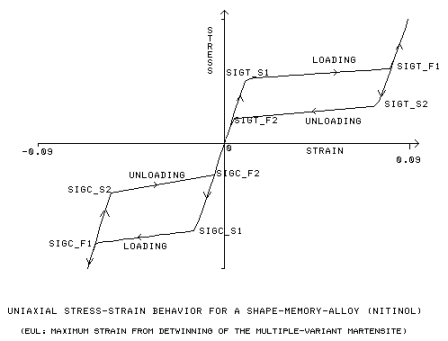
|
σst1, σft1
|
Initial and Final yield stress for tensile loading
[SIGT_S1, SIGT_F1]
|
|
σst2, σft2
|
Initial and Final yield stress for tensile unloading
[SIGT_S2, SIGT_F2]
|
|
σsc1, σfc1
|
Initial and Final yield stress for compressive loading
[SIGC_S1, SIGC_F1]
|
|
σsc2, σfc2
|
Initial and Final yield stress for compressive unloading
[SIGC_S2, SIGC_F2]
|
|
eul
|
(Maximum Tensile Plastic Strain) *(3/2)0.5
|
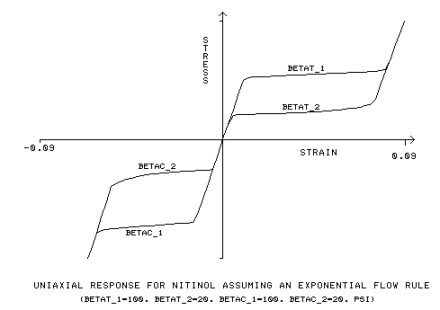
The exponential
flow rule, utilizes additional input constants, β
t1,
β
t2, β
c1, β
c2:
|
βt1
|
material parameter, measuring the speed of
transformation for tensile loading, [BETAT_1]
|
|
βt2
|
material parameter, measuring the speed of
transformation for tensile unloading, [BETAT_2]
|
|
βc1
|
material parameter, measuring the speed of
transformation for compressive loading, [BETAC_1]
|
|
βc2
|
material parameter, measuring the speed of
transformation for compressive unloading, [BETAC_2]
|
The Yield Criterion
To model the possibility of pressure-dependency of the
phase-transformation, a Drucker-Prager-type loading function is used for the yield
criterion:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RIf = 0
where
σ(bar) = effective stress
p = mean stress (or hydrostatic pressure)
α = sqrt(2/3) (σsc1 -
σst1 ) / (σsc1 + σst1)
RfI = [ σfI(sqrt(2/3) + α)], I = 1 for loading and 2 for unloading