In contrast to an isotropic material, an orthotropic material has preferred directions of strength which are mutually perpendicular. The properties along these directions (also known as principal directions) are the extreme values of elastic coefficients.
The [D] matrix for an orthotropic material has nine independent elastic properties. In addition, there are three properties for the thermal expansion.
2-D Orthotropic Stress-Strain Relations
In two dimensions, the orthotropic stress-strain relations can be
written as follows, including temperature effects:
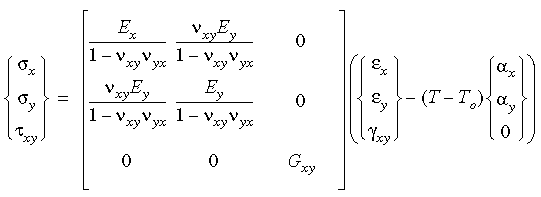
Note that in order to satisfy symmetry
in the matrix of elastic moduli, νxy Ey = νyx Ex.
You need to satisfy the foregoing symmetry
condition when you input the numerical values of either the elastic modulus or
Poisson's ratio.
Further, if you do not input the numerical
value of the shear modulus, the program will compute it as shown below:
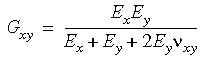
In three
dimensions, the orthotropic symmetry conditions dictate:
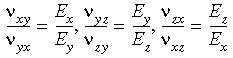
When you
input the orthotropic material properties in three dimensions, you must therefore
make sure that the above symmetry conditions are not violated.
If you enter
the numerical values for the shear moduli (Gxy, Gyz, and
Gxz), the program will use these user-defined values (even if they
are not compatible with the orthotropic symmetry conditions).
Note that if you do not input the numerical values of shear moduli, the program
will compute them using the relations shown below:
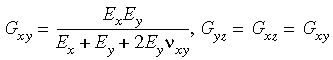
If Ex = Ey = Ez, the program calculates the shear moduli internally even if explicitly
defined.
The program assumes 0.0 for Poisson's ratios that are
not explicitly defined.