1自由度系（Single Degree of Freedom (SDOF) Systems）
簡単なスプリング質量系について考えてみます。質量 (m) は 時間の関数として、U方向にF(t) の力が作用します。質量は u 方向にのみ移動できるため、1自由度系（Single-Degree-Of-Freedom (SDOF) system）と呼びます。運動はスプリングの剛性 (k) による抵抗力が作用します。
この系のニュートンの第2法則（力=質量x加速度）を時間(t)の関数で表すと：
F(t)-ku(t) = mu..(t)
または
mu..(t) + ku(t) = F(t)
ここで、
u..(t) は時間 (t) における質量の加速度であり、時間に対して u の2次導関数に等しい
k = スプリングの剛性
論理的には、質量が変位し解放された場合は、質量は同じ振幅でいつまでも振動を続けることになります。実際には、質量は動きが止まるまで減少する振幅で振動します。この現象を減衰と呼びます。これは摩擦やその他の作用でエネルギーが消費されるために起こります。減衰は複雑な現象です。ここでは、減衰効果が速度に比例するとします。この種類の減衰は粘性減衰（viscous damping）と呼びます。
減衰効果を考慮すると上記の式は次のようになります:
mu..(t) + cu.(t) + ku(t) = F(t)
ここで、
u.(t) は時間 (t) における質量の速度であり、時間に対して u の1次導関数に等しい
静解析スタディでは、速度と加速度は微々たるものとして無視され、F と u は時間の関数とされません。上記の式は次のようになります:F=ku
多自由度系（Multi Degree of Freedom (MDOF) Systems）
多自由度系、m、c、k は単一の値ではなく行列となり、運動方程式は次のようになります:
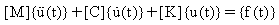
ここで、
[M]: 質量マトリックス
[K] :剛性マトリックス
[C] :減衰マトリックス
{u(t)}:時間 t における変位ベクトル（各節点における変位）
: 時間 t における加速度ベクトル（各節点における加速度）
: 時間 t における速度ベクトル（各節点における速度）
{f(t)}:時変荷重ベクトル （各節点における力）