Ogden ひずみエネルギー密度関数は、次のように定義されます。
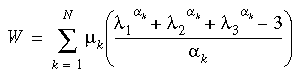
ここで、 λi は主伸張、αi、μi は材料定数、N は関数に含まれる項数です。この関数は、ゴムのような材料の大きな変形範囲を記述する最も優れた関数の 1 つであると考えられています。
Ogden モデルの方程式で使用されるペナルティ関数は、Mooney-Rivlin モデルと同じ形式です。実際に使用されるひずみエネルギー関数は、Ogden関数を修正したものです:
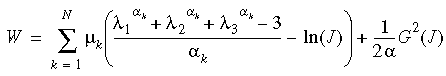
ここで、J は変形体積から変形前体積の比率、N は関数に含まれる項数、G(J) = J2-1、および
 ν はポアソン比です。
ν はポアソン比です。
3 項 (修正されたOgden) モデルが一般に使用されています。プログラムでは 4 項モデル (N=4) までを使用できます。
上記の材料定数に加えて、ポアソン比も必要とされます。多くの場合、ポアソン比を 0.49 から 0.499 に定義することにより満足のいく結果を得ることができます。加えて、かなりの容量ひずみを伴わない限りポアソン比の増加は数値的な結果に著しく影響しません。
ポアソン比が 0.5 に極端に近づいた場合、剛性マトリックス内の負の対角項または収束されないため、解析終了の原因となることがあります。
Ogden モデルの材料特性は、
材料 ダイアログ ボックスで入力されます。 必要な数量は、次のとおりです:
- 1 ~ 4 番目の出力材料係数(αi)
- 1 ~ 4 番目の材料定数(μi)(定数の数に依存)。
- ポアソン比