Układ równań ruchu liniowego układu o n stopniach swobody wzbudzonego przez siłę zmienną w czasie:
 (Równanie 1)
(Równanie 1)
Używając przekształcenia współrzędnych, zbiór n równań równoważnych upraszcza się do n niezależnych równań (każde równanie może zostać rozwiązane niezależnie):
 dla r = 1, 2, ...., n (Równanie 2)
dla r = 1, 2, ...., n (Równanie 2)
gdzie xr(t) są modalnymi współrzędnymi związanymi z modalnymi współrzędnymi ur(t) w następujący sposób:
 (Równanie 3).
(Równanie 3).
Wektor modalnych obciążeń {m(t)} jest określany jako:
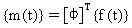 (Równanie 4).
(Równanie 4).
Zakładając, że wzbudzenia są wyrażone przy użyciu funkcji gęstości widmowej mocy (PSD), rozwiązanie można sformułować w dziedzinie częstotliwości. Jeżeli macierz wzbudzeń PSD jest określona jako [Sf(ω)], macierz modalnych sił PSD jest zdefiniowana jako:
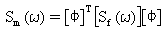 (Równanie 5).
(Równanie 5).
Gęstość widmowa mocy (PSD) modalnej reakcji przemieszczenia [Sx(ω)] jest uzyskiwana ze wzoru:
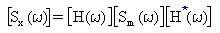 (Równanie 6),
(Równanie 6),
gdzie [H(ω)] jest macierzą modalnej funkcji przeniesienia, a [H*(ω)] jest jej zespolonym sprzężeniem. W przypadku modów normalnych macierz funkcji przeniesienia jest diagonalna, z elementami diagonalnymi Hr(ω).
 (Równanie 7) i
(Równanie 7) i
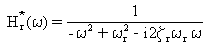 (Równanie 8).
(Równanie 8).
Gęstość widmowa mocy (PSD) reakcji przemieszczenia [Su(ω)] jest następnie wyprowadzana z (Równania 3).
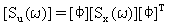 (Równanie 9).
(Równanie 9).
Gęstości widmowe mocy (PSD) reakcji prędkości i przyspieszenia są wyrażone jako:
 (Równanie 10) i
(Równanie 10) i
 (Równanie 11).
(Równanie 11).
Gęstości widmowe mocy (PSD) modalnej prędkości i przyspieszenia są związane z PSD modalnego przemieszczenia w następujący sposób:
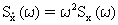 (Równanie 12) oraz
(Równanie 12) oraz 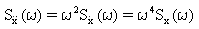 (Równanie 13)
(Równanie 13)
Równanie 10 oraz Równanie 11 można następnie przekształcić do postaci:
 (Równanie 14) oraz
(Równanie 14) oraz  (Równanie 15).
(Równanie 15).
Reakcje modalnej autokorelacji przy zerowym opóźnieniu (τ=0) jako gęstości widmowe mocy (PSD) reakcji modalnej są obliczane z całek:
 (Równanie 16)
(Równanie 16)
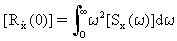 (Równanie 17)
(Równanie 17)
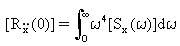 (Równanie 18).
(Równanie 18).
Z powyższych równań obliczane są reakcje średniokwadratowe na podstawie diagonalnych członów macierzy:
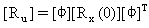 (Równanie 19),
(Równanie 19),
 (Równanie 20),
(Równanie 20),
 (Równanie 21).
(Równanie 21).
Średniokwadratowa reakcja naprężenia
Naprężenia elementu {σ} są określane na podstawie przemieszczeń węzłowych {u} przy użyciu wzoru:
 (Równanie 22) lub jako przemieszczeń modalnych {x} ze wzoru:
(Równanie 22) lub jako przemieszczeń modalnych {x} ze wzoru:
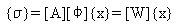 (Równanie 23), gdzie [Φ] jest macierzą wektorów własnych.
(Równanie 23), gdzie [Φ] jest macierzą wektorów własnych.
Macierz korelacji naprężeń [Rσ] jest wyrażona wzorem:
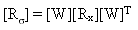 (Równanie 24).
(Równanie 24).