Układ równań ruchu liniowego układu o n stopniach swobody wzbudzonego przez siłę zmienną w czasie:
(Równanie 1)
gdzie:
[M] = symetryczna macierz bezwładności n x n
[M] = symetryczna macierz tłumienia n x n
[K] = symetryczna macierz sztywności n x n
{f(t)} = n-wymiarowy wektor siły
{u},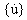 
i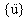 
są odpowiednio n-wymiarowymi wektorami przemieszczenia, prędkości i przyspieszenia.
(Równanie 1) jest układem n równoważnych zwykłych równań różniczkowych ze stałymi współczynnikami. Równania ruchu są sprzężone za pośrednictwem masy, sztywności i tłumienia. Sprzężenie zależy od układu współrzędnych użytego do matematycznego opisania równań ruchu.
Podstawą analizy modalnej jest przekształcenie sprzężonego układu (Równanie 1) w zbiór równań niezależnych poprzez użycie macierzy modalnej [Φ] jako macierzy transformacji. [Φ] zawiera normalne mody {f}i dla i = 1, ...., n uporządkowane jako:
(Równanie 2)
Normalne mody i wartości własne układu są wyprowadzone z rozwiązania problemu wartości własnych:
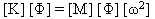(Równanie 3)
gdzie [ω2] jest macierzą diagonalną kwadratów częstotliwości drgań własnych.
Dla układów liniowych, układ n równań ruchu może zostać rozprzężony do n równań pojedynczych stopni swobody względem wektora modalnego przemieszczenia {x}:
(Równanie 4)
Podstawienie wektora {u} z (Równania 4) i przemnożenie go przez [Φ]T (Równanie 1) daje:
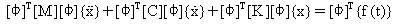(Równanie 5)
Mody normalne spełniają właściwość ortogonalności, a macierz modalna [Φ] jest normalizowana tak, aby była zgodna z następującymi równaniami:
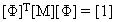(Równanie 6)
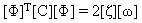(Równanie 7) i
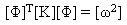(Równanie 8).
Podstawiając (Równania.6--8), (Równanie 5) staje się układem niezależnych równań różniczkowych drugiego stopnia SDOF.
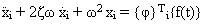dla i =1, ..., n (Równanie 9)
(Równanie 9) jest rozwiązywane przy użyciu takich krokowych metod całkowania, jak Wilson-Theta czy Newmark.
Całkowanie wykonywane jest w dziedzinie, gdzie wyniki ostatniego kroku są używane do przewidzenia wyników następnego kroku.
Wektor przemieszczenia układu (u) jest wyprowadzany z (Równania 4).