Симметричная матрица демпфирования [C] n x n сформулирована в качестве линейной комбинации матриц масс [M] и жесткости [K]:
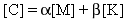(Уравнение 1).
-
Коэффициент Альфа: Устанавливает коэффициент пропорциональности массы α.
-
Коэффициент Бета: Устанавливает коэффициент пропорциональности жесткости β.
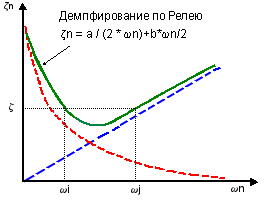
Тип демпфирования, описанный в (Уравнении 1), называется демпфирование по Релею или пропорциональное демпфирование.
Настоящая форма [C] является ортогональной по отношению к системе собственных векторов.
После применения модального преобразования координат матрица модального демпфирования [c] становится диагональной:
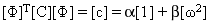(Уравнение 2).
Можно определить демпфирование по Релею для линейных и нелинейных динамических исследований.
Отношение коэффициентов Релея и коэффициента модального демпфирования
Матрица модального демпфирования [c] получается из:
(Уравнение 3).
Коэффициент вязкостного демпфирования ci для i-той моды подсчитан по:
(Уравнение 4),
и коэффициент вязкостного демпфирования ζi выражается как:
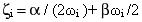(Уравнение 5).
Если коэффициент демпфирования для i-той и j-той мод являются ζi и ζj, то коэффициенты по Релею α и β рассчитываются с помощью решений алгебраических уравнений.
(Уравнение 6).
Если обе моды имеют одинаковый коэффициент демпфирования ( ζi = ζj = ζ), то значения α и β получаются из:
(Уравнение 7) 
(Уравнение 8)
Коэффициент вязкостного демпфирования ζ любой другой моды изменяется с частотой, как показано на рисунке:
