Внутренние силы в том или ином теле меняются от одной точки к другой. По всякой малой внутренней плоской области нагрузки вызываются частью тела на одной стороне такой области в отношении части на другой стороне. Напряжение обозначает интенсивность этих термических сил (сила на единичную площадку).
Напряжение
В непрерывном теле напряжение в точке можно вычислить следующим образом:
- Представьте произвольную плоскость, пересекающую тело в такой точке.
- Рассмотрите бесконечно малую площадь ΔA вокруг этой точки на плоскости.
- Предположим, что величина силы, передаваемой через ΔA в определенном направлении, равна ΔF.
- Тогда напряжение в этом направлении равно ΔF/ΔA по мере приближения ΔA к 0.
Выше приведено определение напряжения или вектора тягового усилия в точке. Состояния напряжение в точке определяется не только вектором тягового усилия. Изменения также зависят от выбранной произвольной плоскости. Тензор напряжения, например, истинный тензор напряжения, определенный как σ = n.T (матричное умножение), где n – это вектор нормали, связанный с плоскостью, и Т – это напряжение или вектор тягового усилия, однозначно определяет напряжение.
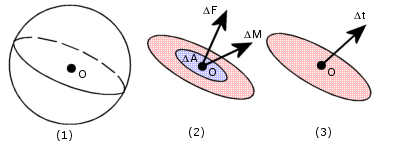
Рисунок (1): Плоскость, проходящая через точку O и разделяющая тело на две части.
Рисунок (2): Векторы результирующей силы и момента в районе области ΔA около точки O в плоскости.
Рисунок (3): Вектор ограничивающего сжатия в точке O на плоскости.
Напряжение
Деформация представляет собой отношение изменения длины δL к исходной длине L. Деформация является безразмерной величиной.
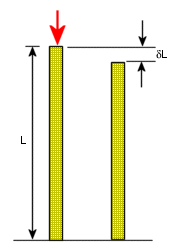
Деформация = δL/L
Последовательность вычислений
Если задана модель с сеткой и набором ограничений перемещения и нагрузок, то программа линейного статического анализа поступает следующим образом.
- Программа составляет и решает систему линейных совместных уравнений равновесия конечных элементов для вычисления составляющих перемещения в каждом узле.
- Далее использует результаты по перемещениям для расчета составляющих деформации.
- Программа использует результаты расчета деформации и отношение напряжение-деформация для вычисления напряжений.

Расчеты напряжений
Результаты расчета напряжений сначала вычисляются в специальных точках, называемых гауссовыми точками или точками квадратуры, расположенными внутри каждого элемента. Эти точки выбираются таким образом. чтобы получить оптимальные числовые результаты. Программа вычисляет напряжения в узлах каждого элемента при помощи экстраполирования результатов, доступных в гауссовых точках.
После успешного запуска, становятся доступными в базе данных результаты узловых напряжений в каждом узле каждого сеточного элемента. Узлы, общие для двух или более элементов, имеют множественные результаты. В общем, эти результаты не являются идентичными, так как метод конечных элементов является приближенным методом. Если, например, некий узел являются общим для трех элементов, могут быть получены три слегка отличающихся значения для каждого компонента в такой точке.
При просмотре результатов по напряжениям, вам могут понадобиться элементные напряжения или узловые напряжения. Для вычисления элементных напряжений программа усредняет соответствующие узловые напряжения для каждого элемента. Для расчета узловых напряжений программа усредняет соответствующий результат по всем элементам, делящим между собой такую узловую точку.