La matriz de amortiguamiento simétrico n x n [C] se formula como una combinación lineal de matrices de masa [M] y rigidez [K]:
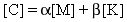(Ecuación 1)
-
Coeficiente alfa: Establece el coeficiente proporcional a la masa α.
-
Coeficiente beta: Establece el coeficiente proporcional a la rigidez β.
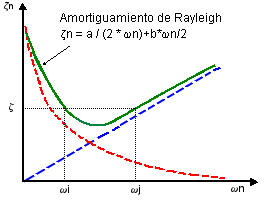
El tipo de amortiguamiento descrito en (Ecuación 1) se conoce como amortiguamiento de Rayleigh o proporcional.
Esta forma de [C] es ortogonal con respecto a los autovectores del sistema.
Si aplicamos la transformación de coordenadas modal, la matriz de amortiguamiento modal [c] se convierte en diagonal:
(Ecuación 2)
Puede definir el amortiguamiento de Rayleigh para estudios dinámicos lineales y no lineales.
Relación de los coeficientes de Rayleigh y el cociente de amortiguamiento modal
La matriz de amortiguamiento modal [c] viene dada por:
(Ecuación 3)
El coeficiente de amortiguamiento viscoso ci para el modo ith se calcula así:
(Ecuación 4)
y el cociente de amortiguamiento viscoso ζi se expresa como
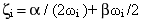(Ecuación 5)
Si los cocientes de amortiguamiento para el modo ith y jth son ζi y ζj, los coeficientes de Rayleigh α y β se calculan a partir de la solución de estas dos ecuaciones algebraicas:
(Ecuación 6)
Si ambos modos tienen el mismo cociente de amortiguamiento ( ζi = ζj = ζ), los valores de α y β vienen dados por:
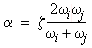(Ecuación 7) 
(Ecuación 8)
El cociente de amortiguamiento viscoso ζ para cualquier otro modo varía con la frecuencia, como se muestra en la figura:
