In linearen statischen Analysen werden die Lasten langsam und schrittweise angewendet, bis sie ihre volle Stärke erreichen. Nach dem Erreichen der vollen Stärke bleiben die Lasten konstant (zeitinvariant). Die Beschleunigungen und Geschwindigkeiten des erregten Systems sind vernachlässigbar gering. In der Formel werden weder Trägheits- noch Dämpfungskräfte berücksichtigt:

wobei:
[K] : Steifigkeits-Matrix
{u}: Verschiebungsvektor
{f}: Lastvektor
Die Lösung produziert Verschiebungen, Spannungen, die konstant sind.
In linearen dynamischen Analysen sind die angewendeten Lasten zeitabhängig. Die Lasten können deterministisch (periodisch, nicht periodisch) oder nicht-deterministisch sein, was bedeutet, dass sie nicht genau vorhergesagt aber statistisch beschrieben werden können. Die Beschleunigungen und Geschwindigkeiten des erregten Systems sind signifikant. In der Formel sollten Trägheits- noch Dämpfungskräfte berücksichtigt werden:
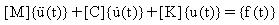
wobei:
[K] : Steifigkeits-Matrix
[C] : Dämpfungsmatrix
[M]: Massenmatrix
{u(t)}: zeitvariierender Verschiebungsvektor
 : zeitvariierender Beschleunigungsvektor
: zeitvariierender Beschleunigungsvektor
 : zeitvariierender Geschwindigkeitsvektor
: zeitvariierender Geschwindigkeitsvektor
{f(t)}: zeitvariierender Lastvektor
Die Reaktion des Systems wird in Zeithistorien (Amplituden versus Zeit) oder in Frequenzspektren (Spitzenwerte versus Frequenz) angegeben.
In linearen dynamischen Analysen variieren die Masse-, Steifigkeits- und Dämpfungsmatrizen nicht mit der Zeit.
Materialeigenschaften werden als linear angenommen. Nicht-lineare dynamische Studien müssen verwendet werden, Nicht-Linearität beim Material vorliegt.
Im Allgemeinen können Sie statische Bedingungen annehmen, wenn die Frequenz von Lasten viel niedriger ist als die niedrigste Eigenfrequenz des Systems.