通过谐波分析,可以计算由于谐波载荷或基准激发而产生的稳态峰值响应。
谐波载荷 P 被表示为 P = A sin (ωt + φ),其中:A 代表振幅,ω 代表频率,t 代表时间,φ 代表相位角度。下面是不同频率 w 随时间变化的谐波载荷范例:
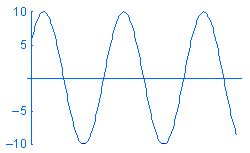
尽管可以创建一个模态时间历史算例并将载荷定义为时间的函数,但您可能对随时间变化的响应的瞬态变化并没有兴趣。 在这种情况下,可以通过谐波分析,求解计算出所需工作频率范围内的稳态峰值响应,从而节省时间和资源。
例如装配在测试台上的马达会通过螺栓将谐波载荷传递给支撑系统。您可以对支撑系统进行建模,并定义一个谐波算例来评估马达工作频率范围内的稳态峰值位移、应力等。您可以按分布质量模拟马达。
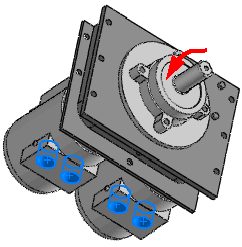
运行算例后,您可以查看响应参数(应力、位移、加速度和速度)的峰值振幅,以及响应参数(超过工作频率范围)的相位角度的响应图表。
在运行谐波算例时,响应参数的轮廓图解在特定的频率步长上显示响应正弦时间历史记录的绝对峰值。 响应参数的瞬态正弦部分及其相位角度未显示在图解中。 对于接近模型的固有频率的工作频率步长,该模式形状的图解是变形形状的更现实展示(与在该特定频率下的位移轮廓图解相比)。
您可以为所有求解频率步长上的响应参数(位移,应力,速度或加速度)创建相位角度的响应图表。
模态、瑞利和复合模态阻尼选项可用于这种分析。