La fonction de densité d'énergie de déformation d'Ogden, exprimée ainsi :

où: λi représente les étirements principaux, αi, μi représentent des constantes de matériau et N représente le nombre de termes dans la fonction, est considérée comme l'une des fonctions les plus efficaces pour définir la plage de grande déformation des matériaux du type caoutchouc.
La fonction de pénalité utilisée dans la formulation du modèle d'Ogden prend la forme de celle qui est utilisée dans le modèle de Mooney-Rivlin. La fonction d'énergie de déformation utilisée est un type modifié de la fonction d'Ogden :
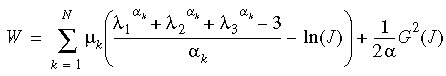
où J représente le rapport du volume déformé au volume non déformé, N est le nombre de termes dans la fonction, G(J) = J2-1, et
 où ν est le coefficient de Poisson.
où ν est le coefficient de Poisson.
Les modèles à trois termes (Ogden modifié) sont fréquemment utilisés. Le programme dispose également de modèles à quatre termes (N=4).
En plus des constantes de matériau mentionnées ci-dessus, le coefficient de Poisson est requis. Dans la plupart des cas, des résultats satisfaisants peuvent être obtenus en affectant un coefficient de Poisson entre 0,49 et 0,499. L'augmentation du coefficient de Poisson n'a aucun effet significatif sur les résultats numériques, à moins qu'une déformation volumétrique importante ne se produise.
Un coefficient de Poisson très proche de 0,5 peut entraîner l'arrêt de la résolution en raison des termes diagonaux négatifs dans la matrice de raideur ou du manque de convergence.
Les propriétés du matériau pour le modèle d'Ogden sont spécifiées dans la boîte de dialogue
Matériau. Les quantités requises sont les suivantes :
- Coefficients de matériau de puissance 1 à 4 (αi)
- Constantes de matériau 1 à 4 (μi) (selon le nombre de constantes).
- Coefficient de Poisson