단일 자유도(SDOF) 시스템
단순 질량-스프링 시스템을 생각해 봅시다. 질량(m)은 u 방향에서 시간의 영향을 받는 힘 F(t)입니다. 질량은 u 모양으로만 움직임 방향이 제한되기 때문에 단일 자유도 (SDOF) 시스템이 됩니다. 모션은 강성 스프링 (k)에 의해 저항을 받습니다.
시간 (t)에서 이 시스템을 위한 뉴튼 제2의 법칙 (힘=질량x시간 가속도)을 쓴다면:
F(t)-ku(t) = mu..(t)
또는:
mu..(t) + ku(t) = F(t)
여기에서,
u..(t)는 시간 (t)에서의 질량의 가속이며 시간에 따른 u의 이차 도함수와 같아집니다.
k = 스프링 강성
이론상, 질량이 변위되어 이동하게 되면 그 질량은 영구히 같은 폭으로 진동하게 되어질 것입니다. 그러나 실제 그 질량은 점차 진동의 진폭이 작아지면서 멈추게 됩니다. 이러한 현상을 댐핑이라하며 마찰이나 다른 원인으로 인한 에너지 손실에 따른 결과입니다. 댐핑은 매우 복잡한 현상입니다. 이를 다루기 위해서, 이 댐핑의 정도가 속도에 비례한다고 가정합시다. 이러한 종류의 댐핑을 점성 댐핑이라 합니다.
댐핑을 고려한다면, 위의 방정식은 다음과 같습니다.
mu..(t) + cu.(t) + ku(t) = F(t)
여기에서,
u..(t)는 시간(t) 에서의 질량의 속도이며 시간에 따른 U의 일차 도함수와 같아집니다.
정적 해석 스터디에서, 속도와 가속도는 무시될 정도로 너무 작아서 F and u 는 시간의 함수가 되지 못합니다. 따라서 위의 식에서 F=ku 가 됩니다.
다중 자유도(SDOF) 시스템
다중 자유도 시스템(MDOF) 에서는 m, c, k 는 모션에서의 단일값이 아닌 행열이 되면 그러한 모션의 수식은 다음과 같이 나타내집니다.
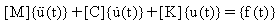
여기에서,
[M]: 질량 행렬
[K] : 강성 행렬
[C] : 감쇠 행렬
{u(t)}: 시간 t 에서 디스플레이스먼트 벡터 (모든 node의 디스플레이스먼트 요소)
: 시간 t에서 가속 벡터(모든 node의 가속 요소)
: 시간 t에서 속도 벡터(모든 node의 속도 요소)
{f(t)}: 시간이력 하중 벡터 (모든 node 의 힘의 요소)