降伏準則可如下式表示: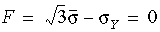
其中
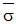
是有效應力,σ
Y 是從單軸向測試中得出的降伏應力。 von Mises 模型可用來描述金屬的行為。 使用此材料模型時,應注意下列幾項考量點:
- 如有使用小位移或大位移時,則假設具有小應變。
- 包含相關的流動律假定。
- 等向及動性硬化定律均可使用。當在偏向空間中的降伏曲面的半徑及中心可相對於負載歷程變化時,會套用等向及動性硬化的線性組合。
參數RK 定義等向及動性硬化的比例。對於純粹的等向硬化,參數 RK 有 0 的值。降伏曲面的半徑伸展,但其中心仍保持固定在偏向空間中。對於純粹的動性硬化,參數 RK 有 1 的值。降伏曲面的半徑保持固定,但其中心可在偏向空間中移動。
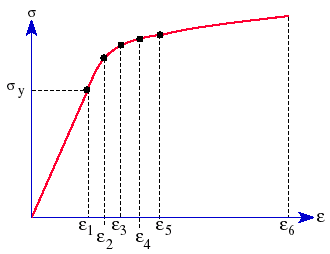
可輸入可塑性的雙線性或多線性單軸向應力 - 應變曲線。 在雙線性應力-應變曲線定義中,可透過材料對話方塊,輸入降伏強度、彈性模數、相切模數。 在多線性應力-應變曲線定義中,應定義應力-應變曲線。
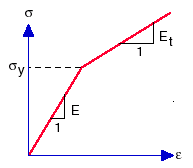
定義應力-應變曲線時,曲線上的第一個點應為材料的降伏點。材料屬性如彈性模數、降伏強度等,會於應力-應變曲線成立時從中取得,而非擷取自材料對話方塊中的材料屬性。只有 Poisson 比 (NUXY) 會從該屬性表中擷取。
落下測試研究僅能使用可塑性的雙線性應力-應變曲線。 如果您定義多線性應力-應變曲線並執行落下測試研究,求解器會予以忽略。
雙線性應力-應變曲線描述中的降伏強度及彈性模數參數可與溫度曲線建立關聯性,以執行熱塑性分析。熱塑性不適用於薄殼元素。
Huber-von Mises 模型可應用於實體 (粗略和精細品質) 及厚殼 (粗略和精細品質) 元素。
建議使用 NR (Newton-Raphson) 迭代法。
塑膠材料的典型應力 - 應變曲線: