На основе данной кривой усталостного напряжения материала S-N можно вычислить производные констант уравнения Басквина. Также программа может вычислить константы Басквина автоматически, если указано число точек данных на кривой S-N, которые будут использоваться в вычислениях аппроксимации кривой.
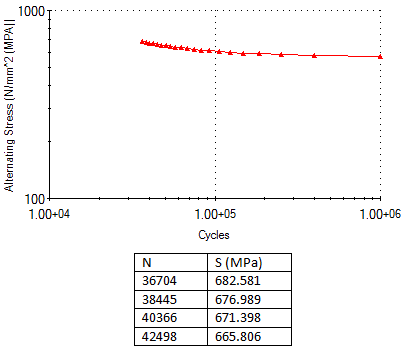
Для некоторых материалов, доступных в базе материалов SOLIDWORKS и на веб-портале материалов SOLIDWORKS, указаны данные кривой усталостного напряжения S-N. Например, кривая S-N материала Ti-6AI-4V (альфа-бета титановый сплав), загруженного с веб-портала материалов SOLIDWORKS (в базе материалов используется формат *.sldmat), отображена на двойной логарифмической шкале log S - log N.
Числовые значения первых четырех точек данных S-N приведены в таблице.
Уравнение Басквина представляет собой степенную зависимость, описывающую линейное соотношение между примененными циклами напряжения (S) по оси y и числом циклов до разрушения по оси x, отображенными на двойной логарифмической шкале.
Эта зависимость имеет следующий вид:
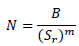
где N — число циклов до разрушения (как правило, более 104) , Sr — эталонное значение концентрации напряжений (в Simulation это диапазон напряжений, в качестве которого берется 2-кратное переменное напряжение), m — наклон кривой двойного логарифмического отношения усталостных напряжений log S - log N, а B — значение напряжения в одном цикле.
Для вычисления наклона m графика уравнения Басквина необходимо решить систему уравнений:
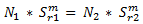
Для определения значения m требуется вычислить значение логарифма для обоих выражений:
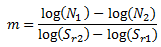
Подставьте первые две точки данных S-N из вышеприведенной таблицы и вычислите сначала значение m, а затем значение B:
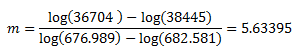

При вычислении константы B программа использует значение диапазона напряжений (от максимального циклического напряжения до минимального циклического напряжения). Если значения напряжений кривой S-N заданы как переменные напряжения (что является типичным случаем), для вычисления константы B необходимо умножить эти напряжения на 2 (диапазон напряжений = 2* переменное напряжение, при условии нулевого среднего напряжения и полного реверсирования циклической нагрузки). Если данные кривой S-N заданы как значения диапазона напряжений, для вычисления константы B подставьте эти данные непосредственно в уравнение. При вычислении константы наклона m умножение напряжений не меняет значение наклона.
На вкладке
Кривые усталости SN (в диалоговом окне
Материал) введите значение B в поле
Константа кривой (B) и значение m в поле
Наклон кривой S-N (m) . Выберите соответствующие единицы измерения напряжений в поле
Единицы и снимите флажок
Вычислять константы Басквина на основе кривой S-N.
Также графики кривой усталостного напряжения можно найти в стандартах, таких как Eurocode 9: Конструкции алюминиевые. Расчёт параметров и конструктивные особенности, EN 1999-1-3:2007/A1.
Пример кривой усталостного напряжения S-N
В стандарте Eurocode 9 указаны числовые значения наклона кривой m для различных категорий деталей. Эти значения можно использовать для вычисления константы B.
Например, в Табл. J.2 - Категории деталей для плоских сочленений, EN 1999-1-3:2007/A1 для простой пластины с отверстиями указан диапазон напряжений Ds = 100 МПа при N = 2x106 циклах и наклоне кривой m = 7; при этом значение B равно:
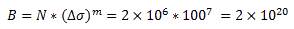
Для автоматического выполнения аппроксимации кривой к прямой линии на основе имеющегося набора данных S-N выберите Вычислять константы Басквина на основе кривой S-N. В этом случае необходимо убедиться, что для параметра Интерполировать задано значение Log-log, а в поле Использовать точку отсечки на кривой S-N из строки выбрана последняя расчетная точка данных S-N.
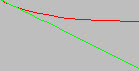
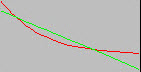
Два графика показывают наложение исходной кривой S-N (выделена красным цветом) на линию аппроксимации кривой уравнения Басквина (выделена зеленым цветом) для 2 (a) и 22 (б) точек данных S-N соответственно. Перед началом анализа рекомендуется проверить качество аппроксимации кривой Басквина. Наилучшее качество линии аппроксимации исходной кривой S-N достигается на фрагменте кривой S-N до точки среза.
|
|
| (a) Аппроксимация кривой Басквина с 2 точками данных S-N (выделена зеленым цветом). |
(б) Аппроксимация кривой Басквина с 22 точками данных S-N (выделена зеленым цветом). |