拓撲的最小最大公式

在零組件上使用多個負載情況時，您可以在拓撲研究中使用最小最大公式。

當您把零組件受制於多個負載情況時，最佳化目標為最佳勁度重量比的最小最大公式會設法個別針對每個負載情況，盡量提高零組件的勁度或是盡量降低屈從性。

例如，受制於三個獨立負載情況的零組件，特定質量減輕限制的最佳勁度重量比的標準最佳化公式會設法盡量降低總屈從性。 屈從性是衡量一個結構的整體彈性或柔軟性的標準，而且是勁度的倒數。 總屈從性是三個屈從性 C1、C2 和 C3 的總和，每個負載情況分別計算。

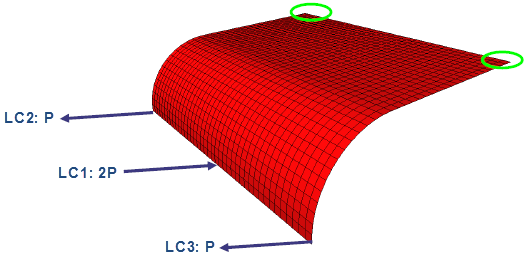
平板的薄殼網格模型使用三個獨立的負載情況載入： LC1、LC2 和 LC3。在角落的六種自由度已固定。

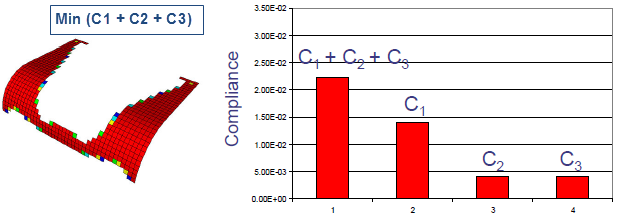標準公式產生的最佳化形狀。 在 40% 質量減輕限制之下的最小最佳化目標 (C1 + C2 +C3)。

最小最大最佳化公式設法盡量降低每個負載情況分別計算的最大屈從性，並盡量提高每個負載情況的零組件勁度。 零組件的最佳化形狀擁有每個可以獨立運作的負載情況的最大勁度。

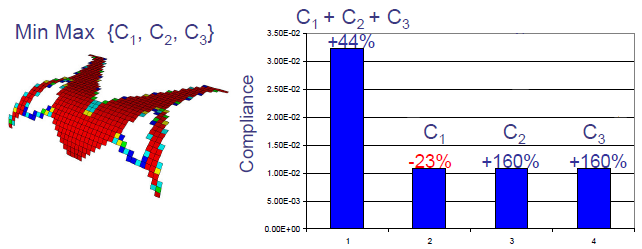最小最大公式產生的最佳化形狀。 在 40% 質量減輕限制之下的最小最大最佳化目標 {C1 + C2 +C3}。 最佳化形狀中每個獨立的負載情況均有相等的勁度。