Proces losowy lub stochastyczny
Na proces stochastyczny można spojrzeć jak na rodzinę zmiennych losowych lub zbór dużej liczby rekordów, które opisują zjawisko fizyczne. Rekordy te mogą być funkcją czasu {xk(t)} lub częstotliwości {xk(f)}. Każdy rekord różni się w jakiś sposób od wszystkich innych rekordów. Dlatego też nie jest możliwe uwzględnienie w analizie wszystkich możliwych rekordów. Zamiast tego dokonuje się opisu procesu losowego poprzez właściwości statystyczne. Każde obciążenie w badaniu drgań losowych jest procesem losowym. Reakcja modelu na te obciążenia również jest procesem losowym opisanym statystycznie.
Funkcja autokorelacji
Funkcja autokorelacji procesu losowego opisuje korelację pomiędzy wartościami w rekordzie w różnych chwilach czasowych. Jest ona definiowana jako wartość oczekiwana iloczynu zmiennej losowej x(t) z przesuniętą w czasie wartością tej zmiennej.
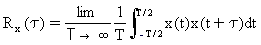 (Równanie 1)
(Równanie 1)
Średnia kwadratowa (RMS)
Wartość średnia kwadratów stanowi miarę energii skojarzonej z procesem losowym.
Jest ona zdefiniowana jako wartość funkcji autokorelacji dla τ = 0
 (Równanie 2)
(Równanie 2)
gdzie E nosi nazwę operatora oczekiwania. Dodatni pierwiastek kwadratowy tej wartości średniej to średnia kwadratowa lub RMS.
Wariancja
Wartość średniej kwadratowej procesu losowego względem jego średniej μx.
 (Równanie 3)
(Równanie 3)
Dodatni pierwiastek kwadratowy wariancji to odchylenie standardowe.
Gęstość widmowa mocy (PSD)
Gęstość widmowa mocy jest definiowana jako transformacja Fouriera funkcji autokorelacji procesu losowego.
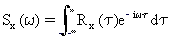 (Równanie 4)
(Równanie 4)
Gęstość widmowa mocy opisuje rozkład energii procesu losowego w dziedzinie częstotliwości.
Biały szum
Sygnał białego szumu posiada jednorodną gęstość widmową mocy dla wszystkich częstotliwości. Innymi słowy energia sygnału jest jednakowo rozłożona dla wszystkich częstotliwości.