Description
Calculate the deflection at the center of a simply supported isotropic plate subjected to:
- Concentrated load F = 400 lbs, and
- Uniform pressure q = 1 psi.
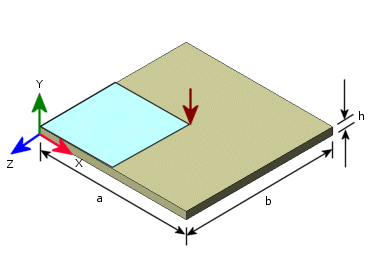
Dimensions of the plate are as follows: h = 1 in, a = b = 40 in.
File Name
Browse to drive
letter:\Users\Public\Public Documents\SOLIDWORKS\SOLIDWORKS
version\samples\Simulation
Examples\Verification\Static_1.SLDPRT and open the
file.
Shell Parameters
Shell thickness is 1" - Thin formulation.
Material Properties
Modulus of elasticity = 3 X 107 psi, Poisson's ratio = 0.3.
Meshing Parameters
Use the default Global Size for Study A and 1/2 the Global Size (left-most position on the slider) for Study B.
Modeling Hints
Due to double symmetry in geometry and loads, only a quarter of the plate is modeled.
Results
The deflection at the center of the plate is calculated and compared to analytical solution.
| Case |
X (in) |
Y (in) |
Deflection at
the center (UY), in |
| Theory |
SOLIDWORKS Simulation |
| Maximum Study A |
20 |
20 |
0.00270230 |
0.00270293 |
| Maximum Study B |
20 |
20 |
0.00378327 |
0.00378550 |
Analytical Solution
Study A: UY = (0.0116 * F * b2) / D
D = (E * h3) / (12* (1 - v2))
Study B: UY = ( 0.00406 * q * b4) / D
where:
-
F: Concentrated load
- q: Uniform pressure
- b: Plate side
-
E: Modulus of Elasticity
- v: Poisson's ratio
- h: Plate thickness
Reference
Timoshenko, S. P. and Woinowsky-Krieger, “Theory of Plates and Shells,” McGraw-Hill Book Co., 2nd edition. pp. 120, 143, 1962.