Dämpfungseffekte
Wenn Sie Anfangsbedingungen auf ein dynamisches System anwenden, vibriert
das System mit abnehmenden Amplituden, bis es zu einem Stillstand kommt.
Dieses Phänomen wird als Dämpfung bezeichnet. Dämpfung ist ein komplexes
Phänomen, das Energie über viele Mechanismen wie interne und externe Reibung,
Wärmeeffekte von zyklisch elastischen Dehnmaterialien auf mikroskopischer
Ebene und Luftwiderstand zerstreut.
Es ist schwierig, Zerstreuungsmechanismen mathematisch zu beschreiben.
Dämpfungseffekte werden für gewöhnlich in idealisierten mathematischen
Formeln dargestellt. In einigen Fällen werden Dämpfungseffekte durch äquivalente
viskose Dämpfer angemessen beschrieben.
Ein viskoser Dämpfer (oder Dämpfungsglied)
erzeugt eine Kraft, die proportional zur Geschwindigkeit ist. Ein Kolben,
der sich frei in einem Zylinder bewegen kann und mit einer zähflüssigen
Flüssigkeit wie Öl gefüllt ist, ist ein Beispiel für einen viskosen Dämpfer.
Von der Dämpfungskraft Fd
wird angenommen, dass sie linear auf die relative Geschwindigkeit an den
beiden Enden des Dämpfers ist:
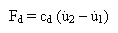(Gleichung 1).
Die Konstante cd, die die
Neigung der Kurve Fd
versus der relativen Geschwindigkeit ist, wird als Koeffizient
der kritischen Dämpfung bezeichnet;
Die Einheiten des Koeffizienten der kritischen Dämpfung sind (Kraft)/(Geschwindigkeit)
oder (Kraft x Zeit)/(Länge).
Die Reaktion eines allgemeinen kritisch gedämpften Systems mit n-Freiheitsgraden
ist angegeben durch:
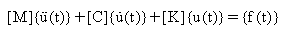(Gleichung
2), wo:
[M] = n
x n symmetrische
Massen- (oder Trägheits)matrix
[C] = n
x n symmetrische
Dämpfungsmatrix
[K] = n
x n symmetrische
Steifigkeitsmatrix
{f(t)} =
n-dimensionaler
Kraftvektor
, 
, 
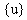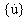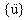sind die n-dimensionalen
Verschiebungs-, Geschwindikeits- und Beschleunigungsvektoren.
Im Allgemeinen führt eine klassische Schwingungsanalyse
nicht unbedingt zu einem unabhängigen System von Bewegungsgleichungen,
es sein den, die Dämpfungsmatrix [c],
die von der modalen Koordinatentransformation resultiert, kann als diagonale
Matrix behandelt werden.
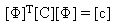(Gleichung 3)
Folgende Dämpfungsarten sind verfügbar:
Siehe auch
Modale
Zeitverlaufsanalyse
Harmonische
Analyse
Zufällige
Vibrationsanalyse