Modelo de material Nitinol

Las aleaciones con memoria de forma (SMA) como Nitinol presentan el efecto superelástico. El término "superelástico" se utiliza para describir materiales con la capacidad de soportar grandes deformaciones en ciclos de cargas y descargas sin mostrar deformaciones permanentes. De hecho, en ciclos de cargas-descargas, incluso hasta deformaciones unitarias de 10-15%, el material muestra una respuesta histerética, una ruta rígida-blanda-rígida para cargas y descargas, sin deformación permanente.

El modelo de material Nitinol está disponible para elementos sólidos y de vaciado.

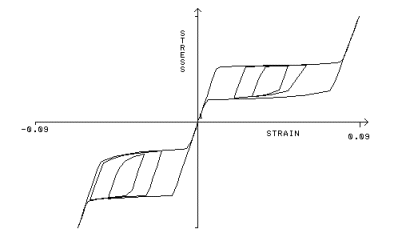
Respuesta de tensión-deformación unitaria típica para una barra de Nitinol en condiciones de carga uniaxial. Observe que el material se comporta de manera diferente en tensión y compresión.

La curva de tensión-deformación unitaria de aleaciones con memoria de forma demuestra un comportamiento macroscópico distintivo, no presente en materiales tradicionales. Este comportamiento se atribuye a la macromecánica subyacente.

Las SMA presentan transformaciones de fase martensítica reversibles; es decir, transformaciones sin difusión de sólido a sólido entre una fase más ordenada desde el punto de vista cristalográfico, "austenita", y una fase menos ordenada desde el punto de vista cristalográfico, "martensita".

Las partes blandas de la curva de respuesta representan las áreas en donde ocurre una transformación de fase, es decir, una conversión de austenita en maternsita (carga) y de martensita en austenita (descarga).

Sin embargo, para evitar complicaciones, nos referiremos al comportamiento blando en la curva de respuesta como “plástico” y a las porciones rígidas como “elásticas”.

Según esta definición, el material primero se comporta de manera elástica hasta alcanzar un determinado nivel de tensión (el límite elástico inicial en la carga). Si la carga continúa, el material muestra un comportamiento elastoplástico hasta que la deformación unitaria plástica alcanza su valor de ruptura. Desde este punto en adelante, el material se comporta nuevamente de manera elástica con cargas aumentadas.

Para descargar, el material nuevamente comienza a descargar elásticamente hasta que la tensión se reduce al límite elástico inicial en la descarga. El material se descargará en forma elastoplástica hasta que se pierda toda la deformación unitaria plástica acumulada (de la fase de carga). Desde este punto en adelante, el material se descargará nuevamente de manera elástica hasta volver a su forma original (sin deformación permanente) y tensión cero con cargas cero.

La fórmula del modelo de Nitinol

Puesto que Nitinol generalmente se utiliza por su capacidad de soportar deformaciones unitarias finitas, se emplea para este modelo la teoría de la gran deformación unitaria mediante deformaciones unitarias logarítmicas junto con la formulación lagrangiana actualizada.

El modelo constitutivo, por lo tanto, se construye para relacionarse con las deformaciones unitarias logarítmicas y los componentes de tensiones de Kirchhoff. Sin embargo, la matriz constitutiva y el vector de deformación unitaria finalmente se transforman para presentar las tensiones de Cauchy (verdaderas).

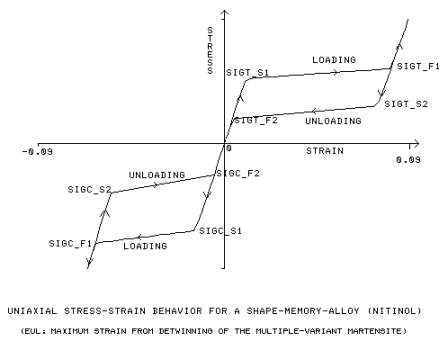
sst1, sft1=Límite elástico inicial y final para límite de tracción. [SIGT_S1, SIGT_F1]

sst2, sft2=Límite elástico inicial y final para descarga de tracción. [SIGT_S2, SIGT_F2]

ssc1, sfc1=Límite elástico inicial y final para límite de compresión. [SIGC_S1, SIGC_F1]

ssc2, sfc2=Límite elástico inicial y final para descarga de compresión. [SIGC_S2, SIGC_F2]

eul = (Deformación unitaria plástica tangencial máxima)(3/2)0.5

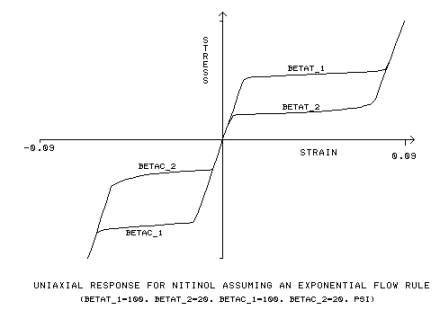
La regla de flujo exponencial utiliza constantes de entrada adicionales, bt1, bt2, bc1, bc2:

bt1 = parámetro de material que mide la velocidad de transformación para el límite de tracción, [BETAT_1]

bt2 = parámetro de material que mide la velocidad de transformación para la descarga de tracción, [BETAT_2]

bc1 = parámetro de material que mide la velocidad de transformación para el límite de compresión, [BETAC_1]

bc2 = parámetro de material que mide la velocidad de transformación para la descarga de compresión, [BETAC_2]

El criterio de flexibilidad

Para modelar la posibilidad de que se produzca una dependencia de la presión por parte de la transformación de fase, se utiliza una función de carga de tipo Drucker-Prager para el criterio de flexibilidad.

 F(t) = sqrt(2) s + 3 a p

 F- Rif = 0

Donde:

s = tensión efectiva

p = tensión media (o presión hidrostática)

a = sqrt(2/3) ( ssc1- sst1) / ( ssc1+ sst1)

Rfi = [ sfi(sqrt (2/3) + a )] : i = 1: carga, i = 2: descarga

La regla de flujo

Mediante la adopción de la definición de deformación unitaria logarítmica, los componentes desviatorios y volumétricos de los tensores de deformación unitaria y tensión pueden expresarse correctamente de forma individual.

Primero, consideramos que los vectores de deformación unitaria plástica y elástica total se presentan de la siguiente manera:

ep = eul xs ( n + a m )

ee = e  - ep

Como resultado, el vector de tensión de Kirchhoff puede evaluarse a partir de:

t = pm + t

p = K ( q - 3 a eulxs)

t = 2G ( e - eul xs n)

En las formulaciones anteriores:

eul = parámetro escalar que representa la deformación unitaria plástica máxima del material [EUL]

xs = parámetro entre cero y uno, como una medida de la deformación unitaria plástica

q =  deformación unitaria volumétrica = e11 + e22 + e33

e = vector de deformación unitaria desviatoria

t = vector de tensión desviatoria

n = norma de la tensión desviatoria: t/(sqrt(2) s) ?

m = la matriz de identidad en forma del vector: {1,1,1,0,0,0}T

K & G = módulos elásticos masivo y de corte: { K = E/[3(1-2n), G = E/[2(1+v)]}

En consecuencia, la regla de flujo lineal en la forma incremental puede expresarse de la siguiente manera:

Carga: Dxs= ( 1.0 - xs)DF / ( F - R1f)

Descarga: Dxs= xs DF / ( F - R2f)

Y la regla de flujo exponencial utilizada cuando se define b distinto de cero:

Carga: Dxs= b1( 1.0 - xs)DF / ( F - R1f)2

Descarga: Dxs= b2xs DF / ( F - R2f)2

Notas:

• En general, las aleaciones con memoria de forma demuestran no ser sensibles a los efectos de la velocidad. Por lo tanto, en la formulación anterior, el “tiempo” representa una pseudovariable y su longitud no afecta a la solución.

• Todas las ecuaciones se presentan aquí para límite de carga-descarga de tracción, puesto que pueden utilizarse expresiones similares (con parámetros de propiedades compresivas) para las condiciones de límites de carga-descarga de compresión.

• El algoritmo de solución incremental aquí presentado utiliza un procedimiento de asignación de retorno en la evaluación de tensiones y ecuaciones constitutivas para un paso de solución. En consecuencia, la solución consta de dos partes. Inicialmente, se calcula un estado de prueba. A continuación, si el estado de prueba infringe el criterio de flujo, se realiza un ajuste para retornar las tensiones a la superficie de flujo.

Referencias:

1. Auricchio, F., “A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model,” International Journal of Plasticity, vol. 17, pp. 971-990, 2001.

2. Auricchio, F.,  Taylor, R.L.,y Lubliner, J., “Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior,”  Computer Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.

3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. “On Large Strain Elasto-Plastic and Creep Analysis,”  Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.

4. Hughes, T., eds. “Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,”  Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, Holanda, 1984.