Modelo viscoelástico
Los materiales elásticos que tienen la capacidad de disipar la energía mecánica debido a efectos viscosos se caracterizan como materiales viscoelásticos. Para un estado de tensión multiaxial, la relación constitutiva puede formularse de la siguiente manera:
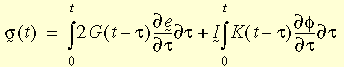
donde e y f son las deformaciones unitarias desviatorias y volumétricas; G(t - t) y K(t - t) son funciones de relajación cortantes y masivas. Las funciones de relajación pueden representarse mediante el modelo mecánico (que se muestra en esta figura) que generalmente se menciona como un Modelo de Maxwell generalizado, expresándose de la siguiente manera:
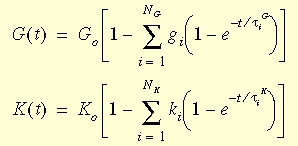
donde G0 y K0 son los módulos cortantes y masivos iniciales (t = 0) proporcionados por: G0 =E/2(1+v) y K0 =E/3(1-2v).
gi, ki, tiG, y tiK son los módulos cortantes y de comprensibilidad i-avo y los tiempos correspondientes.
El efecto de la temperatura en el comportamiento del material se presenta mediante el principio de correspondencia entre tiempo-temperatura. La forma matemática del principio es:
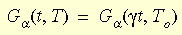
donde g t es el tiempo reducido y g es la función de cambio. La ecuación WLF (Williams-Landel-Ferry) se utiliza para realizar una aproximación de la función:
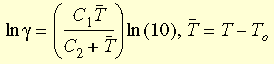
donde TO es la temperatura de referencia que generalmente se selecciona como la Temperatura de transición vítrea; C1 y C2 son constantes dependientes del material.
Entre los parámetros obligatorios, se incluyen los siguientes:
|
Parámetro |
Símbolo |
Descripción |
|
Parámetros elásticos lineales |
EX |
Módulo elástico |
|
NUxy |
Coeficiente de Poisson |
|
GXY (opcional) |
Módulo cortante |
|
Parámetros de función de relajación |
G1, G2, G3,..., G8 |
representan g1, g2,..., g8 en las ecuaciones del Modelo de Maxwell generalizado |
|
TAUG1, TAUG2, ....., TAUG8 |
representan t1g, t2g,..., t8g en las ecuaciones del Modelo de Maxwell generalizado |
|
K1, K2, ..., K8 |
representan k1, k2,..., k8 en las ecuaciones del Modelo de Maxwell generalizado |
|
TAUK1, TAUK2, ..., TAUK8 |
representan t1k, t2k,..., t8k en las ecuaciones del Modelo de Maxwell generalizado |
|
Parámetros de ecuación WLF |
REFTEMP |
representa T0 en la ecuación WLF |
|
VC1 |
representa C1 en la ecuación WLF |
|
VC2 |
representa C2 en la ecuación WLF |
Al definir una curva de relajación cortante o masiva en la pestaña Tablas y curvas, el primer punto de la curva (t =1) es el módulo G1 o K1 en el momento t1. En el momento t = 0, el programa calcula automáticamente G0 o K0 a partir del módulo elástico y el Coeficiente de Poisson.
El modelo de material viscoelástico puede utilizarse con los elementos de vaciado sólido y grueso de alta calidad y calidad de borrador.